 login/create account
login/create account
Recent Activity
4-regular 4-chromatic graphs of high girth ★★
Author(s): Grunbaum
Forcing a $K_6$-minor ★★
Author(s): Barát ; Joret; Wood
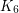 -minor.
-minor. 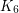 -minor.
-minor. Keywords: connectivity; graph minors
Funcoidal products inside an inward reloid ★★
Author(s): Porton
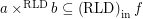 then
then 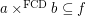 for every funcoid
for every funcoid 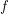 and atomic f.o.
and atomic f.o.  and
and  on the source and destination of
on the source and destination of 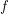 correspondingly.
correspondingly. A stronger conjecture:
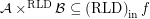 then
then 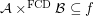 for every funcoid
for every funcoid 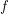 and
and 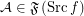 ,
, 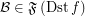 .
. Keywords: inward reloid
Odd cycles and low oddness ★★
Author(s):
 the cycles of any
the cycles of any 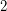 -factor are odd, then
-factor are odd, then 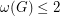 , where
, where 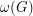 denotes the oddness of the graph
denotes the oddness of the graph  , that is, the minimum number of odd cycles in a
, that is, the minimum number of odd cycles in a  -factor of
-factor of  .
. Keywords:
Odd perfect numbers ★★★
Author(s): Ancient/folklore
Keywords: perfect number
Matching cut and girth ★★
Author(s):
 does there exists a
does there exists a 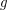 such that every graph with average degree smaller than
such that every graph with average degree smaller than  and girth at least
and girth at least 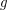 has a matching-cut?
has a matching-cut? Keywords: matching cut, matching, cut
Strong 5-cycle double cover conjecture ★★★
Author(s): Arthur; Hoffmann-Ostenhof
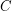 be a circuit in a bridgeless cubic graph
be a circuit in a bridgeless cubic graph  . Then there is a five cycle double cover of
. Then there is a five cycle double cover of  such that
such that 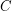 is a subgraph of one of these five cycles.
is a subgraph of one of these five cycles. Keywords: cycle cover
Characterizing (aleph_0,aleph_1)-graphs ★★★
Call a graph an 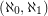 -graph if it has a bipartition
-graph if it has a bipartition 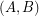 so that every vertex in
so that every vertex in  has degree
has degree 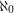 and every vertex in
and every vertex in 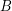 has degree
has degree 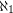 .
.
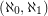 -graphs.
-graphs. Keywords: binary tree; infinite graph; normal spanning tree; set theory
The Berge-Fulkerson conjecture ★★★★
 is a bridgeless cubic graph, then there exist 6 perfect matchings
is a bridgeless cubic graph, then there exist 6 perfect matchings 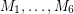 of
of  with the property that every edge of
with the property that every edge of  is contained in exactly two of
is contained in exactly two of 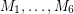 .
.
Keywords: cubic; perfect matching
Obstacle number of planar graphs ★
Author(s): Alpert; Koch; Laison
Does there exist a planar graph with obstacle number greater than 1? Is there some  such that every planar graph has obstacle number at most
such that every planar graph has obstacle number at most  ?
?
Keywords: graph drawing; obstacle number; planar graph; visibility graph
Twin prime conjecture ★★★★
Author(s):
 so that both
so that both  and
and 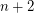 are prime.
are prime.
Keywords: prime; twin prime
Cores of strongly regular graphs ★★★
Keywords: core; strongly regular
Square achievement game on an n x n grid ★★
Author(s): Erickson
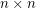 grid. The first player (if any) to occupy four cells at the vertices of a square with horizontal and vertical sides is the winner. What is the outcome of the game given optimal play? Note: Roland Bacher and Shalom Eliahou proved that every 15 x 15 binary matrix contains four equal entries (all 0's or all 1's) at the vertices of a square with horizontal and vertical sides. So the game must result in a winner (the first player) when n=15.
grid. The first player (if any) to occupy four cells at the vertices of a square with horizontal and vertical sides is the winner. What is the outcome of the game given optimal play? Note: Roland Bacher and Shalom Eliahou proved that every 15 x 15 binary matrix contains four equal entries (all 0's or all 1's) at the vertices of a square with horizontal and vertical sides. So the game must result in a winner (the first player) when n=15. Keywords: game
What is the largest graph of positive curvature? ★
Keywords: curvature; planar graph
Extension complexity of (convex) polygons ★★
Author(s):
The extension complexity of a polytope  is the minimum number
is the minimum number 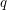 for which there exists a polytope
for which there exists a polytope 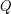 with
with 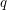 facets and an affine mapping
facets and an affine mapping  with
with 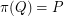 .
.
 , a convex polygon on
, a convex polygon on  vertices whose extension complexity is
vertices whose extension complexity is 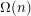 ?
? Keywords: polytope, projection, extension complexity, convex polygon
Strict inequalities for products of filters ★
Author(s): Porton
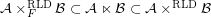 for some filter objects
for some filter objects  ,
, 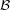 . Particularly, is this formula true for
. Particularly, is this formula true for 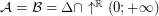 ?
? A weaker conjecture:
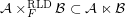 for some filter objects
for some filter objects 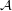 ,
, 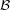 .
. Keywords: filter products
Barnette's Conjecture ★★★
Author(s): Barnette
Keywords: bipartite; cubic; hamiltonian
Covering a square with unit squares ★★
Author(s):
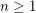 , it is impossible to cover a square of side greater than
, it is impossible to cover a square of side greater than  with
with 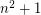 unit squares.
unit squares. Keywords:

 Drupal
Drupal CSI of Charles University
CSI of Charles University