 login/create account
login/create account
infinite graph
Characterizing (aleph_0,aleph_1)-graphs ★★★
Call a graph an 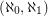 -graph if it has a bipartition
-graph if it has a bipartition 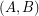 so that every vertex in
so that every vertex in  has degree
has degree 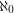 and every vertex in
and every vertex in  has degree
has degree 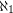 .
.
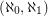 -graphs.
-graphs. Keywords: binary tree; infinite graph; normal spanning tree; set theory
Highly arc transitive two ended digraphs ★★
Author(s): Cameron; Praeger; Wormald
 is a highly arc transitive digraph with two ends, then every tile of
is a highly arc transitive digraph with two ends, then every tile of  is a disjoint union of complete bipartite graphs.
is a disjoint union of complete bipartite graphs. Keywords: arc transitive; digraph; infinite graph
Strong matchings and covers ★★★
Author(s): Aharoni
Let  be a hypergraph. A strongly maximal matching is a matching
be a hypergraph. A strongly maximal matching is a matching 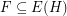 so that
so that 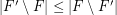 for every matching
for every matching 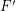 . A strongly minimal cover is a (vertex) cover
. A strongly minimal cover is a (vertex) cover 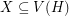 so that
so that 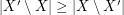 for every cover
for every cover 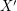 .
.
 is a (possibly infinite) hypergraph in which all edges have size
is a (possibly infinite) hypergraph in which all edges have size 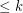 for some integer
for some integer  , then
, then  has a strongly maximal matching and a strongly minimal cover.
has a strongly maximal matching and a strongly minimal cover. Keywords: cover; infinite graph; matching
Unfriendly partitions ★★★
If  is a graph, we say that a partition of
is a graph, we say that a partition of 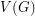 is unfriendly if every vertex has at least as many neighbors in the other classes as in its own.
is unfriendly if every vertex has at least as many neighbors in the other classes as in its own.
Keywords: coloring; infinite graph; partition
Hamiltonian cycles in powers of infinite graphs ★★
Author(s): Georgakopoulos
- \item If
 is a countable connected graph then its third power is hamiltonian. \item If
is a countable connected graph then its third power is hamiltonian. \item If  is a 2-connected countable graph then its square is hamiltonian.
is a 2-connected countable graph then its square is hamiltonian. Keywords: hamiltonian; infinite graph
Hamiltonian cycles in line graphs of infinite graphs ★★
Author(s): Georgakopoulos
- \item If
 is a 4-edge-connected locally finite graph, then its line graph is hamiltonian. \item If the line graph
is a 4-edge-connected locally finite graph, then its line graph is hamiltonian. \item If the line graph 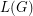 of a locally finite graph
of a locally finite graph  is 4-connected, then
is 4-connected, then 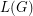 is hamiltonian.
is hamiltonian. Keywords: hamiltonian; infinite graph; line graphs
Infinite uniquely hamiltonian graphs ★★
Author(s): Mohar
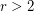 ?
? Keywords: hamiltonian; infinite graph; uniquely hamiltonian
Unions of triangle free graphs ★★★
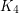 which cannot be expressed as a union of
which cannot be expressed as a union of 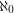 triangle free graphs?
triangle free graphs? Keywords: forbidden subgraph; infinite graph; triangle free
Seymour's self-minor conjecture ★★★
Author(s): Seymour
Keywords: infinite graph; minor

 Drupal
Drupal CSI of Charles University
CSI of Charles University