login/create account
r-regular graphs are not uniquely hamiltonian.
Conjecture If 
is a finite 
-regular graph, where 
, then is not uniquely hamiltonian.
is a finite -regular graph, where 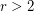, then is not uniquely hamiltonian. (Reproduced from [M].)
A graph is said to be uniquely hamiltonian if it contains precisely one Hamiltonian cycle.
This conjecture has been proved for all odd values of [T] and for all even values of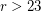 
[H]. By Petersen's theorem, it would suffice to prove it for 
.
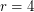Bibliography
[H] P. Haxell, Oberwolfach reports, 2006.
[M] Bojan Mohar, Problem of the Month
*[S] John Sheehan: The multiplicity of Hamiltonian circuits in a graph. Recent advances in graph theory (Proc. Second Czechoslovak Sympos., Prague, 1974), pp. 477-480. Academia, Prague, 1975, MathSciNet
[T] A.G. Thomason, Hamiltonian cycles and uniquely edge colourable graphs. Advances in graph theory (Cambridge Combinatorial Conf., Trinity College, Cambridge, 1977). Ann. Discrete Math. 3 (1978), Exp. No. 13, 3 pp.
* indicates original appearance(s) of problem.
The construction in that
On June 20th, 2022 Anonymous says:
The construction in that paper has parallel edges, so it is not a counter example. As far as I am aware, Sheehan's conjecture is still open.
The conjecture is only for
On May 3rd, 2022 Anonymous says:
The conjecture is only for simple graphs. The paper you mention gives counterexamples that have multiple edges.
Drupal
CSI of Charles University
Is this question still open?
I think, the autor answers the question in this article: Uniqueness of maximal dominating cycles in 3-regular graphs and of hamiltonian cycles in 4-regular graphs (https://doi.org/10.1002/jgt.3190180503). (And the conjecture is fals for all even values.) Am I wrong?