 login/create account
login/create account
hamiltonian
Hamiltonian cycles in powers of infinite graphs ★★
Author(s): Georgakopoulos
Conjecture
- \item If
 is a countable connected graph then its third power is hamiltonian. \item If
is a countable connected graph then its third power is hamiltonian. \item If  is a 2-connected countable graph then its square is hamiltonian.
is a 2-connected countable graph then its square is hamiltonian. Keywords: hamiltonian; infinite graph
Hamiltonian cycles in line graphs of infinite graphs ★★
Author(s): Georgakopoulos
Conjecture
- \item If
 is a 4-edge-connected locally finite graph, then its line graph is hamiltonian. \item If the line graph
is a 4-edge-connected locally finite graph, then its line graph is hamiltonian. \item If the line graph 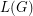 of a locally finite graph
of a locally finite graph  is 4-connected, then
is 4-connected, then 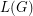 is hamiltonian.
is hamiltonian. Keywords: hamiltonian; infinite graph; line graphs
Hamiltonian cycles in line graphs ★★★
Author(s): Thomassen
Conjecture Every 4-connected line graph is hamiltonian.
Keywords: hamiltonian; line graphs
Infinite uniquely hamiltonian graphs ★★
Author(s): Mohar
Problem Are there any uniquely hamiltonian locally finite 1-ended graphs which are regular of degree 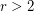 ?
?
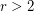 ?
? Keywords: hamiltonian; infinite graph; uniquely hamiltonian
r-regular graphs are not uniquely hamiltonian. ★★★
Author(s): Sheehan
Conjecture If  is a finite
is a finite  -regular graph, where
-regular graph, where 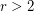 , then
, then  is not uniquely hamiltonian.
is not uniquely hamiltonian.
 is a finite
is a finite  -regular graph, where
-regular graph, where 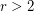 , then
, then  is not uniquely hamiltonian.
is not uniquely hamiltonian. Keywords: hamiltonian; regular; uniquely hamiltonian
Barnette's Conjecture ★★★
Author(s): Barnette
Conjecture Every 3-connected cubic planar bipartite graph is Hamiltonian.
Keywords: bipartite; cubic; hamiltonian
Hamiltonian paths and cycles in vertex transitive graphs ★★★
Author(s): Lovasz
Problem Does every connected vertex-transitive graph have a Hamiltonian path?
Keywords: cycle; hamiltonian; path; vertex-transitive

 Drupal
Drupal CSI of Charles University
CSI of Charles University