 login/create account
login/create account
Hamiltonian paths and cycles in vertex transitive graphs
The question posed here is due to Lovasz [L], but the general problem of finding Hamiltonian paths and cycles in highly symmetric graphs is much older. Knuth has traced it back to bell ringing, and it appears again in gray codes and in the knight's tour of a chessboard.
Vertex-transitive graphs are, of course, very special, very well-behaved graphs, and it seems unsurprising that many of them have Hamiltonian cycles. What is surprising is that there are only five connected ones known which do not have Hamiltonian cycles. This list consists of the complete graph on 2 vertices, the Petersen graph, Coxeter's graph, and the graphs obtained from Petersen and Coxeter by truncating every vertex (inflate each vertex to a triangle). In particular, we do not know of a vertex transitive graph without a Hamiltonian path.
Interestingly, there seems to be considerable disagreement among experts as to what the answer will be. On one hand, there does not appear to be any particular reason why vertex-transitive graphs should almost always have Hamiltonian cycles. On the other hand, such graphs have been studied and searched for at great length, and so far every one investigated with the exception of the five listed above has proved to have a Hamiltonian cycle. Babai formulated the following conjecture which is in quite sharp contrast to the problem above.
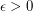 so that there are infinitely many connected vertex-transitive graphs
so that there are infinitely many connected vertex-transitive graphs  with longest cycle of length
with longest cycle of length 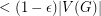 .
. For general vertex-transitive graphs, very little is known. Babai [B79] has shown that a vertex-transitive graph on  vertices has a cycle of length
vertices has a cycle of length 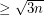 , but (though a very clever arguement) this is obviously quite far from the conjecture. Considerable attention has been given to the special case of Cayley graphs. Here we have the following conjecture.
, but (though a very clever arguement) this is obviously quite far from the conjecture. Considerable attention has been given to the special case of Cayley graphs. Here we have the following conjecture.
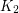 ) has a Hamiltonian cycle.
) has a Hamiltonian cycle. The above conjecture is not difficult to prove for abelian groups. Witte [W] proved it for  -groups, and it has also been established for certain special types of generating sets. Two other results of note are a theorem of Pak-Radocic [PR] showing that every group
-groups, and it has also been established for certain special types of generating sets. Two other results of note are a theorem of Pak-Radocic [PR] showing that every group  has a generating set of size
has a generating set of size 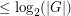 for which the corresponding Cayley graph is Hamiltonian, and a theorem of Krivelevich-Sudakov [KS] showing that almost surely taking a random set of
for which the corresponding Cayley graph is Hamiltonian, and a theorem of Krivelevich-Sudakov [KS] showing that almost surely taking a random set of 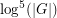 elements of
elements of  as generators yields a Hamiltonian graph.
as generators yields a Hamiltonian graph.
Bibliography
[B79] L. Babai, Long cycles in vertex-transitive graphs. J. Graph Theory 3 (1979), no. 3, 301--304. MathSciNet
[B96] L. Babai, Automorphism groups, isomorphism, reconstruction, in Handbook of Combinatorics, Vol. 2, Elsevier, 1996, 1447-1540. MathSciNet
[KS] M. Krivelevich and B. Sudakov, Sparse pseudo-random graphs are Hamiltonian. J. Graph Theory 42 (2003), no. 1, 17--33. MathSciNet
[L] L. Lov\'{a}sz, "Combinatorial structures and their applications", (Proc. Calgary Internat. Conf., Calgary, Alberta, 1969), pp. 243-246, Problem 11, Gordon and Breach, New York, 1970.
[PR] I. Pak and R. Radocic, Hamiltonian paths in Cayley graphs, preprint
[W] D. Witte, Cayley digraphs of prime-power order are Hamiltonian. J. Combin. Theory Ser. B 40 (1986), no. 1, 107--112. MathSciNet
[WG] D. Witte and J.A. Gallian, A survey: Hamiltonian cycles in Cayley graphs. Discrete Math. 51 (1984), no. 3, 293--304. MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University