 login/create account
login/create account
cycle
Chords of longest cycles ★★★
Author(s): Thomassen
 is a 3-connected graph, every longest cycle in
is a 3-connected graph, every longest cycle in  has a chord.
has a chord. Keywords: chord; connectivity; cycle
What is the smallest number of disjoint spanning trees made a graph Hamiltonian ★★
Author(s): Goldengorin
We are given a complete simple undirected weighted graph 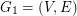 and its first arbitrary shortest spanning tree
and its first arbitrary shortest spanning tree 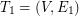 . We define the next graph
. We define the next graph 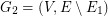 and find on
and find on 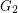 the second arbitrary shortest spanning tree
the second arbitrary shortest spanning tree 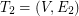 . We continue similarly by finding
. We continue similarly by finding 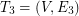 on
on 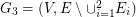 , etc. Let k be the smallest number of disjoint shortest spanning trees as defined above and let
, etc. Let k be the smallest number of disjoint shortest spanning trees as defined above and let 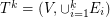 be the graph obtained as union of all
be the graph obtained as union of all  disjoint trees.
disjoint trees.
Question 1. What is the smallest number of disjoint spanning trees creates a graph 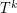 containing a Hamiltonian path.
containing a Hamiltonian path.
Question 2. What is the smallest number of disjoint spanning trees creates a graph 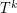 containing a shortest Hamiltonian path?
containing a shortest Hamiltonian path?
Questions 3 and 4. Replace in questions 1 and 2 a shortest spanning tree by a 1-tree. What is the smallest number of disjoint 1-trees creates a Hamiltonian graph? What is the smallest number of disjoint 1-trees creates a graph containing a shortest Hamiltonian cycle?
Keywords: 1-trees; cycle; Hamitonian path; spanning trees
Bigger cycles in cubic graphs ★★
Author(s):
 be a cyclically 4-edge-connected cubic graph and let
be a cyclically 4-edge-connected cubic graph and let  be a cycle of
be a cycle of  . Must there exist a cycle
. Must there exist a cycle 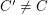 so that
so that 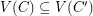 ?
? Antichains in the cycle continuous order ★★
Author(s): DeVos
If  ,
, are graphs, a function
are graphs, a function 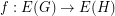 is called cycle-continuous if the pre-image of every element of the (binary) cycle space of
is called cycle-continuous if the pre-image of every element of the (binary) cycle space of  is a member of the cycle space of
is a member of the cycle space of  .
.
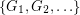 so that there is no cycle continuous mapping between
so that there is no cycle continuous mapping between 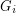 and
and 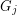 whenever
whenever 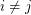 ?
? Hamiltonian paths and cycles in vertex transitive graphs ★★★
Author(s): Lovasz
Keywords: cycle; hamiltonian; path; vertex-transitive
Decomposing eulerian graphs ★★★
Author(s):
 is a 6-edge-connected Eulerian graph and
is a 6-edge-connected Eulerian graph and  is a 2-transition system for
is a 2-transition system for  , then
, then 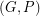 has a compaible decomposition.
has a compaible decomposition. Faithful cycle covers ★★★
Author(s): Seymour
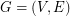 is a graph,
is a graph, 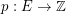 is admissable, and
is admissable, and 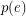 is even for every
is even for every  , then
, then 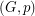 has a faithful cover.
has a faithful cover. (m,n)-cycle covers ★★★
Author(s): Celmins; Preissmann

 Drupal
Drupal CSI of Charles University
CSI of Charles University