 login/create account
login/create account
Cycles
Cycle double cover conjecture ★★★★
(m,n)-cycle covers ★★★
Author(s): Celmins; Preissmann
Faithful cycle covers ★★★
Author(s): Seymour
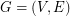 is a graph,
is a graph, 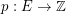 is admissable, and
is admissable, and 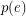 is even for every
is even for every  , then
, then 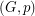 has a faithful cover.
has a faithful cover. Decomposing eulerian graphs ★★★
Author(s):
 is a 6-edge-connected Eulerian graph and
is a 6-edge-connected Eulerian graph and  is a 2-transition system for
is a 2-transition system for  , then
, then 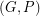 has a compaible decomposition.
has a compaible decomposition. Barnette's Conjecture ★★★
Author(s): Barnette
Keywords: bipartite; cubic; hamiltonian
r-regular graphs are not uniquely hamiltonian. ★★★
Author(s): Sheehan
 is a finite
is a finite  -regular graph, where
-regular graph, where 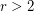 , then
, then  is not uniquely hamiltonian.
is not uniquely hamiltonian. Keywords: hamiltonian; regular; uniquely hamiltonian
Hamiltonian cycles in line graphs ★★★
Author(s): Thomassen
Keywords: hamiltonian; line graphs
Geodesic cycles and Tutte's Theorem ★★
Author(s): Georgakopoulos; Sprüssel
 is a
is a  -connected finite graph, is there an assignment of lengths
-connected finite graph, is there an assignment of lengths 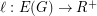 to the edges of
to the edges of  , such that every
, such that every  -geodesic cycle is peripheral?
-geodesic cycle is peripheral? Keywords: cycle space; geodesic cycles; peripheral cycles
Jones' conjecture ★★
For a graph  , let
, let 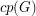 denote the cardinality of a maximum cycle packing (collection of vertex disjoint cycles) and let
denote the cardinality of a maximum cycle packing (collection of vertex disjoint cycles) and let 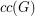 denote the cardinality of a minimum feedback vertex set (set of vertices
denote the cardinality of a minimum feedback vertex set (set of vertices 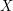 so that
so that 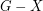 is acyclic).
is acyclic).
 ,
, 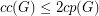 .
. Keywords: cycle packing; feedback vertex set; planar graph
Chords of longest cycles ★★★
Author(s): Thomassen
 is a 3-connected graph, every longest cycle in
is a 3-connected graph, every longest cycle in  has a chord.
has a chord. Keywords: chord; connectivity; cycle
Hamiltonicity of Cayley graphs ★★★
Author(s): Rapaport-Strasser
Keywords:
Strong 5-cycle double cover conjecture ★★★
Author(s): Arthur; Hoffmann-Ostenhof
 be a circuit in a bridgeless cubic graph
be a circuit in a bridgeless cubic graph  . Then there is a five cycle double cover of
. Then there is a five cycle double cover of  such that
such that  is a subgraph of one of these five cycles.
is a subgraph of one of these five cycles. Keywords: cycle cover
Decomposing an eulerian graph into cycles. ★★
Author(s): Hajós
 vertices can be decomposed into at most
vertices can be decomposed into at most 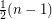 cycles.
cycles. Keywords:
Decomposing an eulerian graph into cycles with no two consecutives edges on a prescribed eulerian tour. ★★
Author(s): Sabidussi
 be an eulerian graph of minimum degree
be an eulerian graph of minimum degree  , and let
, and let 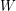 be an eulerian tour of
be an eulerian tour of  . Then
. Then  admits a decomposition into cycles none of which contains two consecutive edges of
admits a decomposition into cycles none of which contains two consecutive edges of 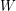 .
. Keywords:
Every prism over a 3-connected planar graph is hamiltonian. ★★
Author(s): Kaiser; Král; Rosenfeld; Ryjácek; Voss
 is a
is a  -connected planar graph, then
-connected planar graph, then 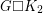 has a Hamilton cycle.
has a Hamilton cycle. Keywords:
4-connected graphs are not uniquely hamiltonian ★★
Author(s): Fleischner
 -connected graph with a Hamilton cycle has a second Hamilton cycle.
-connected graph with a Hamilton cycle has a second Hamilton cycle. Keywords:
Hamilton decomposition of prisms over 3-connected cubic planar graphs ★★
 -connected cubic planar graph can be decomposed into two Hamilton cycles.
-connected cubic planar graph can be decomposed into two Hamilton cycles. Keywords:

 Drupal
Drupal CSI of Charles University
CSI of Charles University