 login/create account
login/create account
Thomassen, Carsten
Partitionning a tournament into k-strongly connected subtournaments. ★★
Author(s): Thomassen
Problem Let  be positve integer Does there exists an integer
be positve integer Does there exists an integer 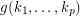 such that every
such that every 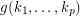 -strong tournament
-strong tournament  admits a partition
admits a partition 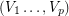 of its vertex set such that the subtournament induced by
of its vertex set such that the subtournament induced by 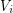 is a non-trivial
is a non-trivial 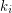 -strong for all
-strong for all 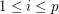 .
.
 be positve integer Does there exists an integer
be positve integer Does there exists an integer 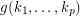 such that every
such that every 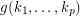 -strong tournament
-strong tournament  admits a partition
admits a partition 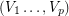 of its vertex set such that the subtournament induced by
of its vertex set such that the subtournament induced by 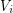 is a non-trivial
is a non-trivial 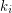 -strong for all
-strong for all 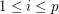 .
. Keywords:
Edge-disjoint Hamilton cycles in highly strongly connected tournaments. ★★
Author(s): Thomassen
Conjecture For every 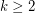 , there is an integer
, there is an integer 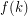 so that every strongly
so that every strongly 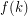 -connected tournament has
-connected tournament has  edge-disjoint Hamilton cycles.
edge-disjoint Hamilton cycles.
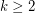 , there is an integer
, there is an integer 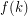 so that every strongly
so that every strongly 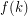 -connected tournament has
-connected tournament has  edge-disjoint Hamilton cycles.
edge-disjoint Hamilton cycles. Keywords:
Subgraph of large average degree and large girth. ★★
Author(s): Thomassen
Conjecture For all positive integers  and
and  , there exists an integer
, there exists an integer  such that every graph of average degree at least
such that every graph of average degree at least  contains a subgraph of average degree at least
contains a subgraph of average degree at least  and girth greater than
and girth greater than  .
.
 and
and  , there exists an integer
, there exists an integer  such that every graph of average degree at least
such that every graph of average degree at least  contains a subgraph of average degree at least
contains a subgraph of average degree at least  and girth greater than
and girth greater than  .
. Keywords:
Arc-disjoint out-branching and in-branching ★★
Author(s): Thomassen
Conjecture There exists an integer  such that every
such that every  -arc-strong digraph
-arc-strong digraph  with specified vertices
with specified vertices  and
and  contains an out-branching rooted at
contains an out-branching rooted at  and an in-branching rooted at
and an in-branching rooted at  which are arc-disjoint.
which are arc-disjoint.
 such that every
such that every  -arc-strong digraph
-arc-strong digraph  with specified vertices
with specified vertices  and
and  contains an out-branching rooted at
contains an out-branching rooted at  and an in-branching rooted at
and an in-branching rooted at  which are arc-disjoint.
which are arc-disjoint.
Keywords:
Counting 3-colorings of the hex lattice ★★
Author(s): Thomassen
Problem Find 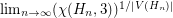 .
.
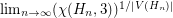 .
. Keywords: coloring; Lieb's Ice Constant; tiling; torus
Chords of longest cycles ★★★
Author(s): Thomassen
Conjecture If  is a 3-connected graph, every longest cycle in
is a 3-connected graph, every longest cycle in  has a chord.
has a chord.
 is a 3-connected graph, every longest cycle in
is a 3-connected graph, every longest cycle in  has a chord.
has a chord. Keywords: chord; connectivity; cycle
The Bermond-Thomassen Conjecture ★★
Conjecture For every positive integer  , every digraph with minimum out-degree at least
, every digraph with minimum out-degree at least 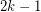 contains
contains  disjoint cycles.
disjoint cycles.
 , every digraph with minimum out-degree at least
, every digraph with minimum out-degree at least 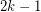 contains
contains  disjoint cycles.
disjoint cycles. Keywords: cycles
Hamiltonian cycles in line graphs ★★★
Author(s): Thomassen
Conjecture Every 4-connected line graph is hamiltonian.
Keywords: hamiltonian; line graphs

 Drupal
Drupal CSI of Charles University
CSI of Charles University