 login/create account
login/create account
cycles
Turán Problem for $10$-Cycles in the Hypercube ★★
Author(s): Erdos
Problem Bound the extremal number of 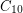 in the hypercube.
in the hypercube.
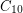 in the hypercube.
in the hypercube. Keywords: cycles; extremal combinatorics; hypercube
Saturation in the Hypercube ★★
Author(s): Morrison; Noel; Scott
Question What is the saturation number of cycles of length 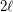 in the
in the  -dimensional hypercube?
-dimensional hypercube?
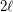 in the
in the  -dimensional hypercube?
-dimensional hypercube? Keywords: cycles; hypercube; minimum saturation; saturation
Cycles in Graphs of Large Chromatic Number ★★
Author(s): Brewster; McGuinness; Moore; Noel
Conjecture If 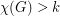 , then
, then  contains at least
contains at least 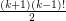 cycles of length
cycles of length 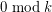 .
.
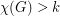 , then
, then  contains at least
contains at least 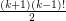 cycles of length
cycles of length 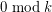 .
. Keywords: chromatic number; cycles
The Bermond-Thomassen Conjecture ★★
Conjecture For every positive integer  , every digraph with minimum out-degree at least
, every digraph with minimum out-degree at least 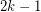 contains
contains  disjoint cycles.
disjoint cycles.
 , every digraph with minimum out-degree at least
, every digraph with minimum out-degree at least 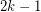 contains
contains  disjoint cycles.
disjoint cycles. Keywords: cycles

 Drupal
Drupal CSI of Charles University
CSI of Charles University