 login/create account
login/create account
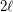 in the
in the  -dimensional hypercube?
-dimensional hypercube?
Let  and
and  be graphs. Say that a spanning subgraph
be graphs. Say that a spanning subgraph 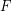 of
of  is
is 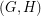 -saturated if
-saturated if 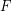 contains no copy of
contains no copy of  but
but 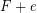 contains a copy of
contains a copy of  for every edge
for every edge 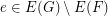 . Let
. Let 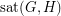 denote the minimum number of edges in a
denote the minimum number of edges in a  -saturated graph. Saturation was introduced by Erdős, Hajnal and Moon [EHM] who proved the following:
-saturated graph. Saturation was introduced by Erdős, Hajnal and Moon [EHM] who proved the following:
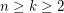 we have
we have 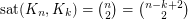 .
. Let 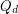 denote the
denote the  -dimensional hypercube. Saturation of
-dimensional hypercube. Saturation of  -cycles in the hypercube has been studied by Choi and Guan [CG] who proved that
-cycles in the hypercube has been studied by Choi and Guan [CG] who proved that 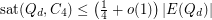 . This was drastically improved by Johnson and Pinto [JP] to
. This was drastically improved by Johnson and Pinto [JP] to 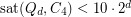 . The saturation number for longer cycles in the hypercube is not known, though. The question above addresses this.
. The saturation number for longer cycles in the hypercube is not known, though. The question above addresses this.
Another open problem is to determine the saturation number of sub-hypercubes in 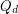 . This was first considered by Johnson and Pinto [JP] who proved that
. This was first considered by Johnson and Pinto [JP] who proved that 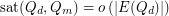 for fixed
for fixed  and
and 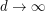 . This upper bound was improved to
. This upper bound was improved to 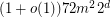 by Morrison, Noel and Scott [MNS]. The best known lower bound on
by Morrison, Noel and Scott [MNS]. The best known lower bound on 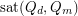 for fixed
for fixed  and large
and large  , also due to [MNS], is
, also due to [MNS], is 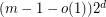 .
.
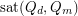 for fixed
for fixed  and large
and large  .
. The results of [MNS] show that 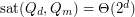 for fixed
for fixed  . Howver, the precise asymptotic behaviour of this quantity is unknown.
. Howver, the precise asymptotic behaviour of this quantity is unknown.
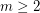 , is it true that
, is it true that 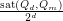 converges as
converges as 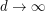 ?
? Bibliography
[CG] S. Choi and P. Guan, Minimum critical squarefree subgraph of a hypercube, Proceedings of the Thirty-Ninth Southeastern International Conference on Combinatorics, Graph Theory and Computing, vol. 189, 2008, pp. 57–64.
[EHM] P. Erdős, A. Hajnal, and J. W. Moon, A problem in graph theory, Amer. Math. Monthly 71 (1964), 1107–1110.
[JP] J. R. Johnson and T. Pinto, Saturated subgraphs of the hypercube, arXiv:1406.1766v1, preprint, June 2014.
[MNS] N. Morrison, J. A. Noel and A. Scott, Saturation in the Hypercube and Bootstrap Percolation, arXiv:1408.5488v2, June 2015.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University