 login/create account
login/create account
Turán Problem for $10$-Cycles in the Hypercube
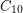 in the hypercube.
in the hypercube.
The problem of bounding the extremal number for cycles in the hypercube was first considered by Erdős [Erd1,Erd2] who conjectured that 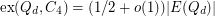 and that
and that 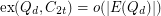 for all
for all 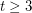 . The first conjecture is still open, and the second is known to be false in the case
. The first conjecture is still open, and the second is known to be false in the case 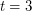 (see [BDT, Chu, Cond]).
(see [BDT, Chu, Cond]).
Chung [Chu] proved that 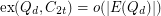 for even
for even 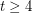 and Füredi and Özkahya [FO1,FO2] proved the same for odd
and Füredi and Özkahya [FO1,FO2] proved the same for odd 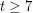 . Conlon [Conl] gave a unified proof of these results, which also applies to more general subgraphs of the hypercube. However, the case of
. Conlon [Conl] gave a unified proof of these results, which also applies to more general subgraphs of the hypercube. However, the case of 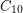 remains unsolved.
remains unsolved.
Bibliography
[BDT] A. E. Brouwer, I. J. Dejter and C. Thomassen, Highly symmetric subgraphs of hypercubes, J. Algebraic Combin. 2 (1993), 25–29.
[Chu] F. Chung, Subgraphs of a hypercube containing no small even cycles, J. Graph Theory 16 (1992), 273–286.
[Cond] M. Conder, Hexagon-free subgraphs of hypercubes, J. Graph Theory 17 (1993), 477–479.
[Conl] D. Conlon, An extremal theorem in the hypercube, Electron. J. Combin. 17 (2010), no. 1, Research Paper 111, 7 pages
[Erd1] P. Erdős, On some problems in graph theory, combinatorial analysis and combinatorial number theory, in: Graph Theory and Combinatorics (Cambridge, 1983), Academic Press, London, 1984, 1–17.
[Erd2] P. Erdős, Some of my favourite unsolved problems, in: A tribute to Paul Erdős, Cambridge University Press, 1990, 467–478.
[FO1] Z. Füredi and L. Özkahya, On 14-cycle-free subgraphs of the hypercube, Combin. Probab. Comput. 18 (2009), 725–729.
[FO2] Z. Füredi and L. Özkahya, On even-cycle-free subgraphs of the hypercube, Electronic Notes in Discrete Mathematics 34 (2009), 515–517.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University