 login/create account
login/create account
hypercube
Weak saturation of the cube in the clique ★
Determine 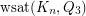 .
.
Keywords: bootstrap percolation; hypercube; Weak saturation
Turán Problem for $10$-Cycles in the Hypercube ★★
Author(s): Erdos
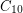 in the hypercube.
in the hypercube. Keywords: cycles; extremal combinatorics; hypercube
Extremal $4$-Neighbour Bootstrap Percolation in the Hypercube ★★
 -neighbour bootstrap process in the hypercube.
-neighbour bootstrap process in the hypercube. Keywords: bootstrap percolation; extremal combinatorics; hypercube; percolation
Saturation in the Hypercube ★★
Author(s): Morrison; Noel; Scott
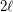 in the
in the  -dimensional hypercube?
-dimensional hypercube? Keywords: cycles; hypercube; minimum saturation; saturation
Coloring squares of hypercubes ★★
Author(s): Wan
If  is a simple graph, we let
is a simple graph, we let 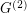 denote the simple graph with vertex set
denote the simple graph with vertex set 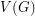 and two vertices adjacent if they are distance
and two vertices adjacent if they are distance 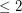 in
in  .
.
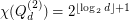 .
. Matchings extend to Hamiltonian cycles in hypercubes ★★
Keywords: Hamiltonian cycle; hypercube; matching
The Crossing Number of the Hypercube ★★
The crossing number 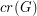 of
of  is the minimum number of crossings in all drawings of
is the minimum number of crossings in all drawings of  in the plane.
in the plane.
The  -dimensional (hyper)cube
-dimensional (hyper)cube 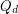 is the graph whose vertices are all binary sequences of length
is the graph whose vertices are all binary sequences of length  , and two of the sequences are adjacent in
, and two of the sequences are adjacent in 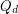 if they differ in precisely one coordinate.
if they differ in precisely one coordinate.
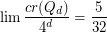
Keywords: crossing number; hypercube

 Drupal
Drupal CSI of Charles University
CSI of Charles University