 login/create account
login/create account
 -neighbour bootstrap process in the hypercube.
-neighbour bootstrap process in the hypercube.
The  -neighbour bootstrap process starts with an initial set of "infected" vertices in a graph and, at each step, a healthy vertex becomes infected if it has at least
-neighbour bootstrap process starts with an initial set of "infected" vertices in a graph and, at each step, a healthy vertex becomes infected if it has at least  infected neighbours. Say that the initial set of infected vertices percolates if every vertex of
infected neighbours. Say that the initial set of infected vertices percolates if every vertex of  is eventually infected. Let
is eventually infected. Let 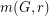 denote the smallest percolating set in
denote the smallest percolating set in  under the
under the  -neighbour process.
-neighbour process.
Let 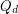 denote the hypercube of dimension
denote the hypercube of dimension  . Balogh and Bollobás [BB] proved the following.
. Balogh and Bollobás [BB] proved the following.
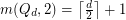 for all
for all 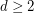 .
. They also conjectured that 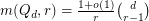 for fixed
for fixed  and
and 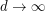 . This conjecture was proved by Morrison and Noel [MN], who also showed the following.
. This conjecture was proved by Morrison and Noel [MN], who also showed the following.
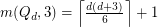 for all
for all 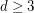 .
. It seems possible that one could obtain a general formula for 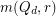 for all
for all  and
and 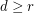 . However, the precise formula for
. However, the precise formula for 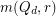 (in terms of
(in terms of  ) is not known for any fixed
) is not known for any fixed 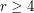 . A solution to this problem may have applications in proving probabilistic results for bootstrap percolation in the hypercube; see [BBM].
. A solution to this problem may have applications in proving probabilistic results for bootstrap percolation in the hypercube; see [BBM].
Bibliography
[BB] J. Balogh and B. Bollobás, Bootstrap percolation on the hypercube, Probab. Theory Related Fields 134 (2006), no. 4, 624–648.
[BBM] J. Balogh, B. Bollobás and R. Morris, Bootstrap percolation in high dimensions, Combin. Probab. Comput. 19 (2010), no. 5-6, 643–692.
[MN] N. Morrison and J. A. Noel, Extremal Bounds for Bootstrap Percolation in the Hypercube, preprint, arXiv:1506.04686v1.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University