Home » Subject » Graph Theory » Coloring » Vertex coloring

Coloring squares of hypercubes (Solved)

Importance: Medium ✭✭
Author(s): Wan, Peng-Jun
Subject: Graph Theory
» Coloring
» » Vertex coloring
Keywords: coloring
hypercube
Recomm. for undergrads: yes
Posted by: mdevos
on: November 21st, 2007
Solved by: See pgregor's reference

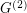If $ G $ is a simple graph, we let $ G^{(2)} $ denote the simple graph with vertex set 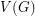$ V(G) $ and two vertices adjacent if they are distance 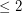$ \le 2 $ in $ G $.

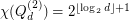Conjecture   $ \chi(Q_d^{(2)}) = 2^{ \lfloor \log_2 d \rfloor + 1} $.

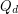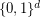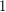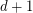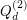Here $ Q_d $, denotes the $ d $-dimensional hypercube, i.e. the graph with vertex set $ \{0,1\}^d $ and two vertices adjacent if they differ in exactly one coordinate. So, the vertices with at most one coordinate equal to $ 1 $ form a clique of size $ d+1 $ in $ Q_d^{(2)} $, giving us the easy lower bound 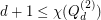$ d+1 \le \chi(Q_d^{(2)}) $. An independent set in 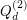$ Q_d^{(2)} $ is precisely an error correcting code, so a proper coloring of this graph may be viewed as a covering of the hypercube with codes. 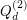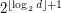Wan [W] constructed a coloring of $ Q_d^{(2)} $ using $ 2^{ \lfloor \log_2 d \rfloor + 1} $ many colors, and he conjectures that this is optimal.

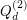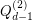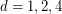Note that $ Q_d^{(2)} $ contains a subgraph isomorphic to $ Q_{d-1}^{(2)} $, so it suffices to prove the conjecture when $ d $ is a power of 2. The cases $ d=1,2,4 $ are rather easy to verify, but 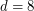$ d=8 $ appears to be open.

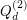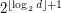In his Ph.D. thesis, Ghebleh suggests the stronger conjecture that $ Q_d^{(2)} $ has circular chromatic number equal to $ 2^{ \lfloor \log_2 d \rfloor + 1} $.

Bibliography

[G] M. Ghebleh, Theorems and Computations in Circular Colourings of Graphs, Ph.D. thesis, Simon Fraser University, 2007.

*[W] P. J. Wan, Near-optimal conflict-free channel set assignments for an optical cluster-based hypercube network. J. Comb. Optim. 1 (1997), no. 2, 179--186. MathSciNet.


* indicates original appearance(s) of problem.
add new comment

disproved

On December 10th, 2008 pgregor says:

Actually, the conjecture is disproved by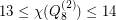 $ 13 \le \chi(Q_8^{(2)}) \le 14 $, obtained independently by Hougardy in 1991 [1] and Royle in 1993 [2, Section 9.7]. Moreover, although not fully determined, it is known that 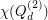$ \chi(Q_d^{(2)}) $ asymptotically attains the lower bound, as 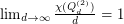$ \lim_{d \to \infty}\frac{\chi(Q_d^{(2)})}{d}=1 $, proven by Ostergard in 2004 [3].

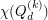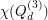There are also several results on $ \chi(Q_d^{(k)}) $ for general $ k $, and in particular on $ \chi(Q_d^{(3)}) $ [3,4].

[1] G.M. Ziegler, Coloring Hamming graphs, optimal binary codes, and the 0/1 Borsuk problem in low dimensions, in: H. Alt (Ed.), Computational Discrete Mathematics, Springer, Berlin, 2001, 159-171.

[2] T.R. Jensen, B. Toft, Graph Coloring Problems, Wiley, New York, 1995.

[3] P.R.J. Ostergard, On a Hypercube coloring problem, J. Combin. Theory A 108 (2004), 199-204.

[4] H.Q. Ngo, D.-Z. Du, R.L. Graham, New bounds on a hypercube coloring problem, Inform. Process. Lett. 84 (2002), 265-269.

reply

Comment viewing options

Select your preferred way to display the comments and click "Save settings" to activate your changes.