 login/create account
login/create account
The Crossing Number of the Hypercube
The crossing number 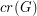 of
of  is the minimum number of crossings in all drawings of
is the minimum number of crossings in all drawings of  in the plane.
in the plane.
The  -dimensional (hyper)cube
-dimensional (hyper)cube 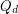 is the graph whose vertices are all binary sequences of length
is the graph whose vertices are all binary sequences of length  , and two of the sequences are adjacent in
, and two of the sequences are adjacent in 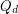 if they differ in precisely one coordinate.
if they differ in precisely one coordinate.
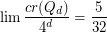
It is known that 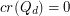 for
for 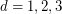 and that
and that 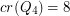 . No other exact values are known. Madej [M] proved that
. No other exact values are known. Madej [M] proved that 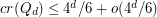 . Faria and de Figueiredo [FF] improved the upper bound to
. Faria and de Figueiredo [FF] improved the upper bound to 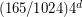 . Sykora and Vrto [SV] proved that
. Sykora and Vrto [SV] proved that 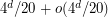 is a lower bound on
is a lower bound on 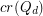 .
.
Bibliography
*[EG] P. Erdős and R.K. Guy, Crossing number problems, Amer. Math. Monthly 80 (1973) 52-58.
[FF] L. Faria, C.M.H. de Figueiredo, On Eggleton and Guy's conjectured upper bound for the crossing number of the  -cube, Math. Slovaca 50 (2000) 271-287.
-cube, Math. Slovaca 50 (2000) 271-287.
[M] T. Madej, Bounds for the crossing number of the  -cube, J. Graph Theory 15 (1991) 81-97.
-cube, J. Graph Theory 15 (1991) 81-97.
[SV] O. Sykora and I. Vrto, On crossing numbers of hypercubes and cube connected cycles, BIT 33 (1993) 232-237.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Improved upper bound
I came accross a paper Faria, Herrera de Figueiredo, Sykora, Vrto: An improved upper bound on the crossing number of the hypercube that proves half of this, getting the correct upper bound.