 login/create account
login/create account
The Crossing Number of the Complete Bipartite Graph
The crossing number 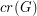 of
of  is the minimum number of crossings in all drawings of
is the minimum number of crossings in all drawings of  in the plane.
in the plane.
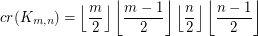
(This discussion appears as [M].)
A drawing of a graph  in the plane has the vertices represented by distinct points and the edges represented by polygonal lines joining their endpoints such that:
in the plane has the vertices represented by distinct points and the edges represented by polygonal lines joining their endpoints such that:
- \item no edge contains a vertex other than its endpoints, \item no two adjacent edges share a point other than their common endpoint, \item two nonadjacent edges share at most one point at which they cross transversally, and \item no three edges cross at the same point.
This problem is also known as Turan's Brickyard Problem (since it was formulated by Turan when he was working at a brickyard - the edges of the drawing would correspond to train tracks connecting different shipping depots, and fewer crossings would mean smaller chance for collision of little trains and smaller chance for their derailing).
This conjectured value for the crossing number of 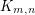 can be realized by the following drawing. Place
can be realized by the following drawing. Place 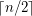 vertices on the positive
vertices on the positive  -axis and
-axis and 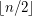 vertices on the negative
vertices on the negative  -axis. Similarly, place
-axis. Similarly, place 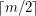 and
and 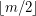 along the positive and negative
along the positive and negative 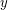 -axis. Now connect each pair of vertices on different axes with straight line segments.
-axis. Now connect each pair of vertices on different axes with straight line segments.
Bibliography
[G] R. Guy, The decline and fall of Zarankiewicz's theorem, in Proof Techniques in Graph Theory (F. Harary Ed.), Academic Press, New York (1969) 63-69.
[K] D. Kleitman, The crossing number of K_{5,n} , J. Combin. Theory 9 (1970) 315-32
[M] B. Mohar, Problem of the Month
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University