 login/create account
login/create account
complete bipartite graph
List Colourings of Complete Multipartite Graphs with 2 Big Parts ★★
Author(s): Allagan
Question Given 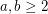 , what is the smallest integer
, what is the smallest integer 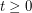 such that
such that 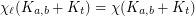 ?
?
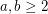 , what is the smallest integer
, what is the smallest integer 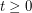 such that
such that 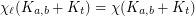 ?
? Keywords: complete bipartite graph; complete multipartite graph; list coloring
Alon-Saks-Seymour Conjecture ★★★
Author(s): Alon; Saks; Seymour
Conjecture If 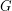 is a simple graph which can be written as an union of
is a simple graph which can be written as an union of  edge-disjoint complete bipartite graphs, then
edge-disjoint complete bipartite graphs, then 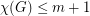 .
.
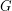 is a simple graph which can be written as an union of
is a simple graph which can be written as an union of  edge-disjoint complete bipartite graphs, then
edge-disjoint complete bipartite graphs, then 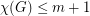 .
. Keywords: coloring; complete bipartite graph; eigenvalues; interlacing
The Crossing Number of the Complete Bipartite Graph ★★★
Author(s): Turan
The crossing number 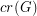 of
of 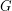 is the minimum number of crossings in all drawings of
is the minimum number of crossings in all drawings of 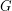 in the plane.
in the plane.
Conjecture 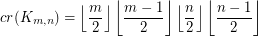
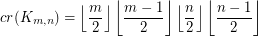
Keywords: complete bipartite graph; crossing number

 Drupal
Drupal CSI of Charles University
CSI of Charles University