 login/create account
login/create account
Turan, Paul
Turán's problem for hypergraphs ★★
Author(s): Turan
Conjecture Every simple  -uniform hypergraph on
-uniform hypergraph on 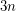 vertices which contains no complete
vertices which contains no complete  -uniform hypergraph on four vertices has at most
-uniform hypergraph on four vertices has at most 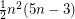 hyperedges.
hyperedges.
 -uniform hypergraph on
-uniform hypergraph on 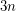 vertices which contains no complete
vertices which contains no complete  -uniform hypergraph on four vertices has at most
-uniform hypergraph on four vertices has at most 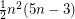 hyperedges.
hyperedges. Conjecture Every simple  -uniform hypergraph on
-uniform hypergraph on 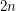 vertices which contains no complete
vertices which contains no complete  -uniform hypergraph on five vertices has at most
-uniform hypergraph on five vertices has at most 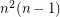 hyperedges.
hyperedges.
 -uniform hypergraph on
-uniform hypergraph on 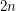 vertices which contains no complete
vertices which contains no complete  -uniform hypergraph on five vertices has at most
-uniform hypergraph on five vertices has at most 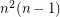 hyperedges.
hyperedges. Keywords:
The Erdos-Turan conjecture on additive bases ★★★★
Let 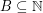 . The representation function
. The representation function 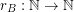 for
for  is given by the rule
is given by the rule 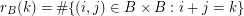 . We call
. We call  an additive basis if
an additive basis if 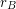 is never
is never  .
.
Conjecture If  is an additive basis, then
is an additive basis, then 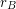 is unbounded.
is unbounded.
 is an additive basis, then
is an additive basis, then 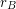 is unbounded.
is unbounded. Keywords: additive basis; representation function
The Crossing Number of the Complete Bipartite Graph ★★★
Author(s): Turan
The crossing number 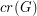 of
of  is the minimum number of crossings in all drawings of
is the minimum number of crossings in all drawings of  in the plane.
in the plane.
Conjecture 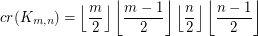
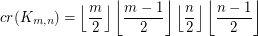
Keywords: complete bipartite graph; crossing number

 Drupal
Drupal CSI of Charles University
CSI of Charles University