 login/create account
login/create account
additive basis
Goldbach conjecture ★★★★
Author(s): Goldbach
Conjecture Every even integer greater than 2 is the sum of two primes.
Keywords: additive basis; prime
The Erdos-Turan conjecture on additive bases ★★★★
Let 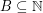 . The representation function
. The representation function 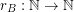 for
for  is given by the rule
is given by the rule 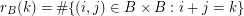 . We call
. We call  an additive basis if
an additive basis if 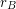 is never
is never  .
.
Conjecture If  is an additive basis, then
is an additive basis, then 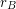 is unbounded.
is unbounded.
 is an additive basis, then
is an additive basis, then 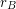 is unbounded.
is unbounded. Keywords: additive basis; representation function
The Alon-Tarsi basis conjecture ★★
Author(s): Alon; Linial; Meshulam
Conjecture If 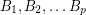 are invertible
are invertible 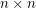 matrices with entries in
matrices with entries in 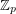 for a prime
for a prime  , then there is a
, then there is a 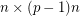 submatrix
submatrix  of
of ![$ [B_1 B_2 \ldots B_p] $](/files/tex/86661dc2948aeca789b4392c2e2a9cbf7d96f735.png) so that
so that  is an AT-base.
is an AT-base.
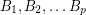 are invertible
are invertible 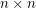 matrices with entries in
matrices with entries in 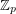 for a prime
for a prime  , then there is a
, then there is a 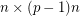 submatrix
submatrix  of
of ![$ [B_1 B_2 \ldots B_p] $](/files/tex/86661dc2948aeca789b4392c2e2a9cbf7d96f735.png) so that
so that  is an AT-base.
is an AT-base. Keywords: additive basis; matrix
The additive basis conjecture ★★★
Author(s): Jaeger; Linial; Payan; Tarsi
Conjecture For every prime  , there is a constant
, there is a constant 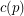 (possibly
(possibly 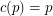 ) so that the union (as multisets) of any
) so that the union (as multisets) of any 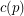 bases of the vector space
bases of the vector space 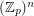 contains an additive basis.
contains an additive basis.
 , there is a constant
, there is a constant 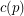 (possibly
(possibly 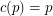 ) so that the union (as multisets) of any
) so that the union (as multisets) of any 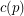 bases of the vector space
bases of the vector space 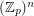 contains an additive basis.
contains an additive basis. Keywords: additive basis; matrix

 Drupal
Drupal CSI of Charles University
CSI of Charles University