Open Problem Garden

Importance: Medium ✭✭

Author(s):	Alon, Noga
	Linial, Nathan
	Meshulam, Roy

Subject:	Combinatorics
	» Matrices

Keywords:	additive basis
	matrix

Recomm. for undergrads: no

Prize: none

Posted	by:	mdevos
	on:	March 8th, 2007

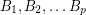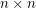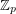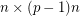Conjecture If $B_1,B_2,\ldots B_p$ are invertible $n \times n$ matrices with entries in ${\mathbb Z}_p$ for a prime $p$ , then there is a $n \times (p-1)n$ submatrix $A$ of $[B_1 B_2 \ldots B_p]$ so that $A$ is an AT-base.

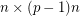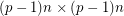Definition: If $A$ is an $n \times (p-1)n$ matrix over a field of characteristic $p$ , then we say that $A$ is an Alon-Tarsi basis (or AT-basis) if the permanent of the $(p-1)n \times (p-1)n$ matrix obtained by stacking 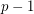$p-1$ copies of $A$ is nonzero.

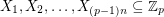It follows from the Alon-Tarsi polynomial technique that if $A$ is an AT-base then for every $X_1,X_2,\ldots,X_{(p-1)n} \subseteq {\mathbb Z}_p$ of size 2 and for every 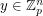$y \in {\mathbb Z}_p^n$ , there exists a vector 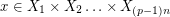$x \in X_1 \times X_2 \ldots \times X_{(p-1)n}$ so that 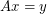$Ax=y$ (using the notation from A nowhere-zero point in a linear mapping, $A$ is (2,1)-choosable). 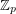It follows from this that every Alon-Tarsi base over ${\mathbb Z}_p$ is also an additive basis. Thus, the above conjecture, if true, would imply The additive basis conjecture. The following strengthening of this conjecture was suggested in [D]

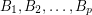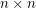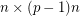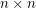Conjecture (The strong Alon-Tarsi basis conjecture (DeVos)) If $B_1,B_2,\ldots,B_p$ are invertible $n \times n$ matrices with entries in a field of characteristic $p$ , then we may partition the columns of $[B_1 B_2 \ldots B_p]$ into an $n \times (p-1)n$ matrix $A$ and an $n \times n$ matrix $C$ so that $A$ is an AT-base and $C$ is invertible.

In addition to implying the conjecture, above, if true, this conjecture would imply both The permanent conjecture and The choosability in 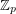${\mathbb Z}_p$ conjecture.

add new comment

Open Problem Garden

Reply

Navigate

Recent Activity