 login/create account
login/create account
Chords of longest cycles
 is a 3-connected graph, every longest cycle in
is a 3-connected graph, every longest cycle in  has a chord.
has a chord. A chord of a cycle  is an edge
is an edge  so that
so that 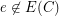 , but both ends of
, but both ends of  are in
are in 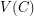 . Longest cycles are of great interest in basic graph theory, and this appealing conjecture suggests a very simple property they should share - at least in 3-connected graphs.
. Longest cycles are of great interest in basic graph theory, and this appealing conjecture suggests a very simple property they should share - at least in 3-connected graphs.
In dense graphs, this conjecture is easy to verify - for instance, if  is Hamiltonian, it is trivially true. More interestingly, Thomassen [T] proved that his conjecture is true for cubic graphs using a clever sufficient condition for Hamiltonicity (based on Thomason's lollipop method) combined with a pretty theorem of Fleischner and Steibitz (cycle plus triangles graphs are 3-colorable).
is Hamiltonian, it is trivially true. More interestingly, Thomassen [T] proved that his conjecture is true for cubic graphs using a clever sufficient condition for Hamiltonicity (based on Thomason's lollipop method) combined with a pretty theorem of Fleischner and Steibitz (cycle plus triangles graphs are 3-colorable).
Other work on this conjecture has focused on graphs embedded in surfaces. Zhang [Z] has proved the conjecture for planar graphs of minimum degree four, Li and Zhang have proved the conjecture for graphs in the projective plane of minimum degree four [LZ1] and for 4-connected graphs in the klein bottle or torus [LZ2]. Finally, Kawarabayashi, Niu, and Zhang [KNZ] have shown the conjecture for 4-connected graphs on a fixed surface with sufficiently high face-width.
Bibliography
[KNZ] K. Kawarabayashi, J. Niu, C. Q. Zhang, Chords of longest circuits in locally planar graphs. European J. Combin. 28 (2007), no. 1, 315--321. MathSciNet
[LZ1] X. Li, C. Q. Zhang, Chords of longest circuits in 3-connected graphs. Discrete Math. 268 (2003), no. 1-3, 199--206. MathSciNet
[LZ2] X. Li, C. Q. Zhang, Chords of longest circuits of graphs embedded in torus and Klein bottle. J. Graph Theory 43 (2003), no. 1, 1--23. MathSciNet.
[T2] C. Thomassen, Chords of longest cycles in cubic graphs. J. Combin. Theory Ser. B 71 (1997), no. 2, 211--214. MathSciNet.
[Z] C. Q. Zhang, Longest cycles and their chords. J. Graph Theory 11 (1987), no. 4, 521--529. MathSciNet.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
New partial results
New partial results for this appear in
Carsten Thomassen: Chords in longest cycles, JCTB 129 (2018) 148-157