 login/create account
login/create account
Minors
Highly connected graphs with no K_n minor ★★★
Author(s): Thomas
Problem Is it true for all 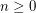 , that every sufficiently large
, that every sufficiently large  -connected graph without a
-connected graph without a 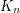 minor has a set of
minor has a set of 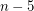 vertices whose deletion results in a planar graph?
vertices whose deletion results in a planar graph?
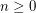 , that every sufficiently large
, that every sufficiently large  -connected graph without a
-connected graph without a 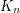 minor has a set of
minor has a set of 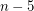 vertices whose deletion results in a planar graph?
vertices whose deletion results in a planar graph? Keywords: connectivity; minor
Seagull problem ★★★
Author(s): Seymour
Conjecture Every  vertex graph with no independent set of size
vertex graph with no independent set of size 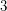 has a complete graph on
has a complete graph on 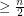 vertices as a minor.
vertices as a minor.
 vertex graph with no independent set of size
vertex graph with no independent set of size 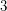 has a complete graph on
has a complete graph on 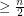 vertices as a minor.
vertices as a minor. Keywords: coloring; complete graph; minor
Forcing a $K_6$-minor ★★
Author(s): Barát ; Joret; Wood
Conjecture Every graph with minimum degree at least 7 contains a 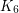 -minor.
-minor.
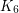 -minor.
-minor. Conjecture Every 7-connected graph contains a 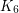 -minor.
-minor.
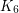 -minor.
-minor. Keywords: connectivity; graph minors
Forcing a 2-regular minor ★★
Conjecture Every graph with average degree at least 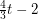 contains every 2-regular graph on
contains every 2-regular graph on 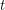 vertices as a minor.
vertices as a minor.
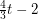 contains every 2-regular graph on
contains every 2-regular graph on 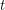 vertices as a minor.
vertices as a minor. Keywords: minors

 Drupal
Drupal CSI of Charles University
CSI of Charles University