Home » Subject » Graph Theory » Basic G.T. » Minors

Forcing a $K_6$-minor

Importance: Medium ✭✭
Author(s): Barát ,János
Joret, Gwenaël
Wood, David R.
Subject: Graph Theory
» Basic Graph Theory
» » Minors
Keywords: connectivity
graph minors
Recomm. for undergrads: no
Posted by: David Wood
on: January 16th, 2012
Conjecture   Every graph with minimum degree at least 7 contains a $ K_6 $-minor.
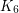Conjecture   Every 7-connected graph contains a $ K_6 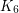$-minor.

The first conjecture implies the second.

Whether the second conjecture is true was first asked in [KT]. Both conjectures were stated in [BJW].

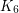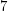The second conjecture is implied by Jørgensen’s conjecture, which asserts that every $ 6 $-connected $ K_6 $-minor-free graph is apex (which have minimum degree at most $ 6 $ and are thus not $ 7 $-connected). Since Jørgensen’s conjecture is true for sufficiently large graphs [KNTWa,KNTWb], the second conjecture is true for sufficiently large graphs.

Related problems

Jorgensen's Conjecture

Bibliography

*[BJW] János Barát, Gwenaël Joret, David R. Wood. Disproof of the List Hadwiger Conjecture, Electronic J. Combinatorics 18:P232, 2011.

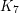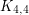*[KT] Ken-ichi Kawarabayashi and Bjarne Toft. Any 7-chromatic graph has $ K_7 $ or $ K_{4,4} $ as a minor. Combinatorica 25 (3), 327–353, 2005.

[KNTWa] Ken-ichi Kawarabayashi, Serguei Norine, Robin Thomas, Paul Wollan. 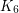$ K_6 $ minors in $ 6 $-connected graphs of bounded tree-width. http://arxiv.org/abs/1203.2171

[KNTWb] Ken-ichi Kawarabayashi, Serguei Norine, Robin Thomas, Paul Wollan. 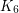$ K_6 $ minors in large $ 6 $-connected graphs. http://arxiv.org/abs/1203.2192


* indicates original appearance(s) of problem.
add new comment