 login/create account
login/create account
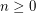 , that every sufficiently large
, that every sufficiently large  -connected graph without a
-connected graph without a 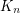 minor has a set of
minor has a set of 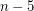 vertices whose deletion results in a planar graph?
vertices whose deletion results in a planar graph? A famous conjecture of Jorgensen asserts that every 6-connected graph without a 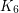 -minor is apex (planar plus one vertex). If true, Jorgensen's conjecture does not generalize (naively) to higher connectivities, since for sufficiently large
-minor is apex (planar plus one vertex). If true, Jorgensen's conjecture does not generalize (naively) to higher connectivities, since for sufficiently large  , there do exist
, there do exist  -connected graphs which are not close to planar in the sense we are considering (many more than
-connected graphs which are not close to planar in the sense we are considering (many more than 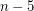 vertices must be deleted to leave a planar graph). This conjecture of Thomas asserts that all such graphs are small in size.
vertices must be deleted to leave a planar graph). This conjecture of Thomas asserts that all such graphs are small in size.
For 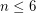 this conjecture is true. For
this conjecture is true. For 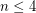 this conjecture is trivial, since any graph without a
this conjecture is trivial, since any graph without a 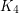 -minor is planar. The
-minor is planar. The 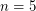 case follows from a theorem of Wagner which gives a construction for all graphs without
case follows from a theorem of Wagner which gives a construction for all graphs without 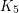 -minors (and from which it follows that every 4-connected graph with no
-minors (and from which it follows that every 4-connected graph with no 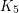 minor is planar). The
minor is planar). The 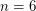 case was recently resolved by DeVos, Hegde, Kawarabayashi, Norine, Thomas, and Wollan. The difficulties associated with finding
case was recently resolved by DeVos, Hegde, Kawarabayashi, Norine, Thomas, and Wollan. The difficulties associated with finding 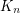 minors in graphs make this conjecture appear daunting, but if true, it would yield powerful insight into the structure of graphs.
minors in graphs make this conjecture appear daunting, but if true, it would yield powerful insight into the structure of graphs.

 Drupal
Drupal CSI of Charles University
CSI of Charles University