 login/create account
login/create account
Jorgensen's Conjecture
For 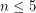 , the class of graphs with no
, the class of graphs with no 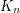 minor is very well understood. Simple graphs without
minor is very well understood. Simple graphs without 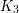 minors are forests. Graphs without
minors are forests. Graphs without 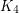 minors are called series-parallel graphs, and have a simple construction. Finally, Wagner [W] obtained a construction for all graphs without
minors are called series-parallel graphs, and have a simple construction. Finally, Wagner [W] obtained a construction for all graphs without 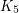 minors. For
minors. For 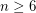 , an explicit characterization of those graphs without
, an explicit characterization of those graphs without 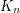 minors appears hopeless. The graph minors project of Robertson and Seymour give a rough structure theorem for such classes, but much remains unknown. In particular, this conjecture and Thomas' conjecture highly connected graphs with no
minors appears hopeless. The graph minors project of Robertson and Seymour give a rough structure theorem for such classes, but much remains unknown. In particular, this conjecture and Thomas' conjecture highly connected graphs with no 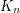 -minor suggest interesting properties of highly connected graphs without
-minor suggest interesting properties of highly connected graphs without 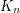 minors which appear quite difficult to resolve.
minors which appear quite difficult to resolve.
Part of the interest in graphs without 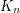 minors stems from Hadwiger's conjecture (every loopless graph without a
minors stems from Hadwiger's conjecture (every loopless graph without a 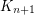 minor is
minor is  -colorable). Indeed, Wagner's work on graphs with no
-colorable). Indeed, Wagner's work on graphs with no 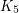 minor was done while studying the
minor was done while studying the 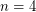 case of Hadwiger. More recently, Robertson, Seymour, and Thomas [RST] proved Hadwiger's conjecture for
case of Hadwiger. More recently, Robertson, Seymour, and Thomas [RST] proved Hadwiger's conjecture for 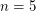 , and in doing so came somewhat close to proving Jorgensoen's conjecture. The thrust of their argument is to prove that any minimal counterexample to Hadwiger for
, and in doing so came somewhat close to proving Jorgensoen's conjecture. The thrust of their argument is to prove that any minimal counterexample to Hadwiger for 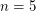 is apex. However, in doing so, they exploit both connectivity and coloring properties of a minimal counterexample. It would appear to be difficult to modify their argument to prove Jorgensen's conjecture.
is apex. However, in doing so, they exploit both connectivity and coloring properties of a minimal counterexample. It would appear to be difficult to modify their argument to prove Jorgensen's conjecture.
DeVos, Hegde, Kawarabayashi, Norine, Thomas, and Wollan proved this conjecture true for all sufficiently large graphs [KNTWa,KNTWb].
Bibliography
[RST] N. Robertson, P. D. Seymour, R. Thomas, Hadwiger's conjecture for 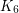 -free graphs. Combinatorica 13 (1993), no. 3, 279-361. MathSciNet
-free graphs. Combinatorica 13 (1993), no. 3, 279-361. MathSciNet
[W] K. Wagner Uber eine Eigenschaft der ebenen Komplexe, Math. Ann 114 (1937) 570-590. MathSciNet
[KNTWa] Ken-ichi Kawarabayashi, Serguei Norine, Robin Thomas, Paul Wollan. 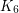 minors in 6-connected graphs of bounded tree-width. J. Combinatorial Theory, Series B, 136:1--32, 2019
minors in 6-connected graphs of bounded tree-width. J. Combinatorial Theory, Series B, 136:1--32, 2019
[KNTWb] Ken-ichi Kawarabayashi, Serguei Norine, Robin Thomas, Paul Wollan. 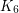 minors in large 6-connected graphs. J. Combinatorial Theory, Series B, 129:158-203, 2019.
minors in large 6-connected graphs. J. Combinatorial Theory, Series B, 129:158-203, 2019.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University