 login/create account
login/create account
 vertex graph with no independent set of size
vertex graph with no independent set of size  has a complete graph on
has a complete graph on 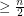 vertices as a minor.
vertices as a minor. This conjecture is significant because it is an interesting unproved consequence of Hadwiger's conjecture (this implication is proved next). In fact, some experts have suggested that this problem might hold the key to finding a counterexample to Hadwiger. I (M. DeVos) have attributed this conjecture to Seymour, but I believe that it may have been independently suggested by Mader and by others. Its curious title will be explained later in this discussion.
Hadwiger's conjecture (every loopless graph with chromatic number 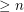 has
has 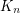 as a minor) is one of the outstanding problems in graph theory. This conjecture has been resolved for small values of
as a minor) is one of the outstanding problems in graph theory. This conjecture has been resolved for small values of  ; when
; when 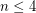 it is relatively easy, for
it is relatively easy, for 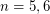 it has been proven to be equivalent to the Four color theorem. The Seagull problem concerns the other extreme - when the size of the chromatic number is close to the order of the graph. If
it has been proven to be equivalent to the Four color theorem. The Seagull problem concerns the other extreme - when the size of the chromatic number is close to the order of the graph. If  is an
is an  vertex graph with no independent set of size 3, then
vertex graph with no independent set of size 3, then 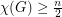 since each color class has size
since each color class has size 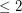 . If Hadwiger's conjecture holds for
. If Hadwiger's conjecture holds for  , it must then have a minor which is a complete graph on
, it must then have a minor which is a complete graph on 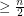 vertices. This is precisely the statement of the Seagull problem.
vertices. This is precisely the statement of the Seagull problem.
The (essentially) best known bound for the conjecture is that every  vertex graph
vertex graph  with no independent set of size 3 has a complete graph on
with no independent set of size 3 has a complete graph on 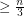 vertices as a minor. This argument is where the name of this conjecture arises. Let us call a seagull of
vertices as a minor. This argument is where the name of this conjecture arises. Let us call a seagull of  an induced subgraph which is a 2-edge path (such a subgraph may be drawn suggestively as a seagull). Then, for every seagull
an induced subgraph which is a 2-edge path (such a subgraph may be drawn suggestively as a seagull). Then, for every seagull  and every vertex
and every vertex  not in
not in  , there must be an edge between
, there must be an edge between  and one of the two endpoints of
and one of the two endpoints of  (this follows from the assumption that
(this follows from the assumption that  has no independent set of size 3). This feature makes seagulls especially useful for constructing complete graphs as minors - as we now demonstrate. Choose a maximal collection
has no independent set of size 3). This feature makes seagulls especially useful for constructing complete graphs as minors - as we now demonstrate. Choose a maximal collection 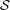 of pairwise disjoint seagulls of
of pairwise disjoint seagulls of  . The graph
. The graph 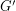 obtained from
obtained from  by deleting every vertex which appears in a seagull in
by deleting every vertex which appears in a seagull in 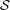 cannot have any two vertices at distance 2 from one another (since this would yield a seagull), so
cannot have any two vertices at distance 2 from one another (since this would yield a seagull), so 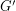 must be a disjoint union of complete graphs. Since
must be a disjoint union of complete graphs. Since 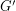 has no independent set of size 3, it is in fact a disjoint union of at most two complete graphs. By deleting every vertex in the smaller complete subgraph of
has no independent set of size 3, it is in fact a disjoint union of at most two complete graphs. By deleting every vertex in the smaller complete subgraph of 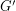 from
from  and then contracting both edges in every seagull in
and then contracting both edges in every seagull in 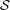 , we obtain a complete graph minor of
, we obtain a complete graph minor of  with size
with size 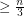 .
.
Kawarabayashi, Plummer, and Toft have improved this bound slightly by showing that  must have a complete graph minor of size
must have a complete graph minor of size 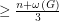 , but it looks very difficult to get much more out of this type of argument.
, but it looks very difficult to get much more out of this type of argument.
Bibliography
[KPT] K. Kawarabayashi, M. Plummer, and B. Toft, Improvements of the theorem of Duchet and Meynial's theorem on Hadwiger's Conjecture, J. Combin. Theory Ser. B. 95 (2005) 152-167.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University