 login/create account
login/create account
Jaeger, Francois
Mapping planar graphs to odd cycles ★★★
Author(s): Jaeger
Conjecture Every planar graph of girth 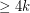 has a homomorphism to
has a homomorphism to 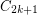 .
.
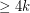 has a homomorphism to
has a homomorphism to 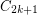 .
. Keywords: girth; homomorphism; planar graph
The additive basis conjecture ★★★
Author(s): Jaeger; Linial; Payan; Tarsi
Conjecture For every prime  , there is a constant
, there is a constant 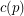 (possibly
(possibly 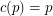 ) so that the union (as multisets) of any
) so that the union (as multisets) of any 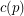 bases of the vector space
bases of the vector space 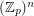 contains an additive basis.
contains an additive basis.
 , there is a constant
, there is a constant 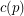 (possibly
(possibly 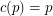 ) so that the union (as multisets) of any
) so that the union (as multisets) of any 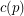 bases of the vector space
bases of the vector space 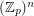 contains an additive basis.
contains an additive basis. Keywords: additive basis; matrix
A nowhere-zero point in a linear mapping ★★★
Author(s): Jaeger
Conjecture If 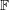 is a finite field with at least 4 elements and
is a finite field with at least 4 elements and  is an invertible
is an invertible 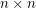 matrix with entries in
matrix with entries in 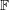 , then there are column vectors
, then there are column vectors 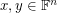 which have no coordinates equal to zero such that
which have no coordinates equal to zero such that 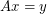 .
.
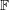 is a finite field with at least 4 elements and
is a finite field with at least 4 elements and  is an invertible
is an invertible 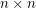 matrix with entries in
matrix with entries in 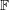 , then there are column vectors
, then there are column vectors 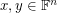 which have no coordinates equal to zero such that
which have no coordinates equal to zero such that 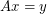 .
. Keywords: invertible; nowhere-zero flow
Jaeger's modular orientation conjecture ★★★
Author(s): Jaeger
Keywords: nowhere-zero flow; orientation

 be a
be a 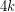 -
-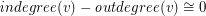 (mod
(mod 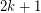 ) for every vertex
) for every vertex  .
.  Drupal
Drupal CSI of Charles University
CSI of Charles University