 login/create account
login/create account
Mapping planar graphs to odd cycles
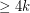 has a homomorphism to
has a homomorphism to 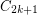 .
. This conjecture is Jaeger's modular orientation conjecture restricted to planar graphs and then dualized. To see this duality, first note that circular coloring and circular flows are dual for planar graphs, and then observe that 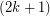 -orientations are equivalent to
-orientations are equivalent to 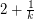 -flows and
-flows and 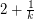 -colorings are equivalent to homomorphisms to
-colorings are equivalent to homomorphisms to 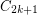 . So if
. So if  and
and 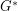 are dual planar graphs, then we have the following equivalences.
are dual planar graphs, then we have the following equivalences.
- \item
 has a
has a 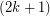 -orientation. \item
-orientation. \item  has a
has a 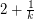 -flow. \item
-flow. \item 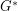 has a
has a 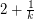 -coloring. \item
-coloring. \item 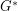 has a homomorphism to
has a homomorphism to 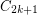 .
. There is an easy family of graphs which show that the above conjecture (if true) is best possible. Let 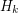 be the graph obtained from an odd circuit of length
be the graph obtained from an odd circuit of length 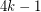 by adding a new vertex
by adding a new vertex  joined to every existing vertex by a path of length
joined to every existing vertex by a path of length 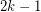 . Now,
. Now, 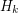 is a planar graph of girth
is a planar graph of girth 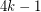 , but there is no homomorphism from
, but there is no homomorphism from 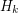 to
to 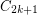 . To see the latter claim, suppose (for a contradiction) that such a homomorphsim
. To see the latter claim, suppose (for a contradiction) that such a homomorphsim  exists, let
exists, let  be the unique circuit of
be the unique circuit of 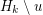 and let
and let  . Now, no vertex in
. Now, no vertex in  can map to
can map to  since every such vertex is distance
since every such vertex is distance 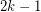 from
from  . However we must then have a homomorphism from
. However we must then have a homomorphism from  to
to  , which is impossible since
, which is impossible since  is an odd circuit and
is an odd circuit and 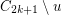 is bipartite.
is bipartite.
The k=1 case of the above conjecture asserts that every (loopless) triangle free planar graph has a homomorphism to the triangle. In other words, every (loopless) triangle free planar graph is 3-colorable. This is a well known theorem of Grotszch. For every k>1, the above conjecture is still open. Actually, I think this conjecture is already quite interesting for k=2. One reason is that this case of the conjecture implies the 5-color theorem for planar graphs. To see this implication, suppose that the above conjecture is true for k=2, let G be a simple loopless planar graph, and let G' be the graph obtained from G by subdividing each edge two times. Now, G' has girth at least 9, so by our assumption there is a homomorphism from G' to C_5. It is easy to see that adjacent vertices of G must map to different vertices of C_5 under this homomorphism. Thus, we have a proper 5-coloring of G as desired.
Let us call a homomorphism to 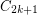 a
a 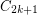 -coloring. It is quite easy to show that every planar graph of girth > 10k has a
-coloring. It is quite easy to show that every planar graph of girth > 10k has a 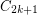 -coloring. This follows from a simple degeneracy argument: Every such (nonempty) graph must have a either a vertex of degree
-coloring. This follows from a simple degeneracy argument: Every such (nonempty) graph must have a either a vertex of degree 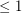 , or a path
, or a path  of length
of length 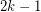 all of whose internal vertices have degree two. Both of these configurations are reducible, in the sense that we may delete either a vertex of degree
all of whose internal vertices have degree two. Both of these configurations are reducible, in the sense that we may delete either a vertex of degree 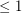 or the interior vertices of
or the interior vertices of  and then extend any
and then extend any 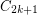 -coloring of the resulting graph to a
-coloring of the resulting graph to a 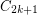 -coloring of the original. By more complicated, but similar degeneracy arguments, we can approach this conjecture. To my knowledge, the best result to date is as follows.
-coloring of the original. By more complicated, but similar degeneracy arguments, we can approach this conjecture. To my knowledge, the best result to date is as follows.
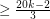 has a homomorphism to
has a homomorphism to 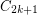 .
. For the special case of the conjecture when 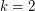 , Matt DeVos and Adam Deckelbaum have an unpublished improvement showing that every planar graph with odd girth
, Matt DeVos and Adam Deckelbaum have an unpublished improvement showing that every planar graph with odd girth 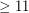 has a homomorphism to
has a homomorphism to 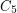 .
.
Bibliography
[BKKW] O. V. Borodin, S. J. Kim, A. V. Kostochka, D. B. West, Homomorphisms from sparse graphs with large girth. Dedicated to Adrian Bondy and U. S. R. Murty. J. Combin. Theory Ser. B 90 (2004), no. 1, 147--159. MathSciNet
[Ja] F. Jaeger, On circular flows in graphs in Finite and Infinite Sets, volume 37 of Colloquia Mathematica Societatis Janos Bolyai, edited by A. Hajnal, L. Lovasz, and V.T. Sos. North-Holland (1981) 391-402.
[Zh] X. Zhu, Circular chromatic number of planar graphs of large odd girth, Electronic Journal of Combinatorics Vol. 8 no. 1 (2001).
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University