 login/create account
login/create account
girth
Colouring $d$-degenerate graphs with large girth ★★
Author(s): Wood
Question Does there exist a  -degenerate graph with chromatic number
-degenerate graph with chromatic number 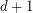 and girth
and girth  , for all
, for all 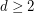 and
and 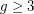 ?
?
 -degenerate graph with chromatic number
-degenerate graph with chromatic number 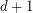 and girth
and girth  , for all
, for all 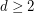 and
and 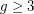 ?
? Keywords: degenerate; girth
Bounding the chromatic number of triangle-free graphs with fixed maximum degree ★★
Conjecture A triangle-free graph with maximum degree  has chromatic number at most
has chromatic number at most 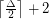 .
.
 has chromatic number at most
has chromatic number at most 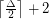 .
.
Keywords: chromatic number; girth; maximum degree; triangle free
4-regular 4-chromatic graphs of high girth ★★
Author(s): Grunbaum
Problem Do there exist 4-regular 4-chromatic graphs of arbitrarily high girth?
Mapping planar graphs to odd cycles ★★★
Author(s): Jaeger
Conjecture Every planar graph of girth 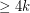 has a homomorphism to
has a homomorphism to 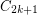 .
.
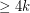 has a homomorphism to
has a homomorphism to 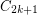 .
. Keywords: girth; homomorphism; planar graph

 Drupal
Drupal CSI of Charles University
CSI of Charles University