 login/create account
login/create account
Bounding the chromatic number of triangle-free graphs with fixed maximum degree
 has chromatic number at most
has chromatic number at most 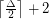 .
.
This conjecture is a special case of Reed's  ,
,  , and
, and 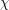 conjecture, which posits that for any graph,
conjecture, which posits that for any graph, 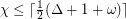 , where
, where  ,
,  , and
, and 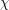 are the clique number, maximum degree, and chromatic number of the graph respectively. Reed's conjecture is very easy to prove for complements of triangle-free graphs, but the triangle-free case seems challenging and interesting in its own right.
are the clique number, maximum degree, and chromatic number of the graph respectively. Reed's conjecture is very easy to prove for complements of triangle-free graphs, but the triangle-free case seems challenging and interesting in its own right.
This conjecture is very much true for large values of  ; Johansson proved that triangle-free graphs have chromatic number at most
; Johansson proved that triangle-free graphs have chromatic number at most 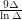 . Surprisingly, the question appears to be open for every value of
. Surprisingly, the question appears to be open for every value of  greater than four, up until Johansson's result implies the conjecture.
greater than four, up until Johansson's result implies the conjecture.
Kostochka previously proved that the chromatic number of a triangle-free graph is at most 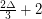 , and he proved that for every
, and he proved that for every 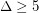 there is a
there is a  for which a graph of girth
for which a graph of girth  has chromatic number at most
has chromatic number at most 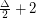 . Specifically, he showed that
. Specifically, he showed that 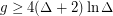 is sufficient. In [K] he posed the general problem: "To find the best upper estimate for the chromatic number of the graph in terms of the maximal degree and density or girth."
is sufficient. In [K] he posed the general problem: "To find the best upper estimate for the chromatic number of the graph in terms of the maximal degree and density or girth."
The conjecture is implied by Brooks' Theorem for 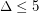 . The three smallest open values of
. The three smallest open values of  offer natural entry points to this problem. The easiest seems to be:
offer natural entry points to this problem. The easiest seems to be:
 -chromatic triangle-free graph of maximum degree 6?
-chromatic triangle-free graph of maximum degree 6? Perhaps looking at graphs of girth at least five would also be a good starting point.
Bibliography
[K] Kostochka, A. V., Degree, girth and chromatic number. Combinatorics (Proc. Fifth Hungarian Colloq., Keszthely, 1976), Vol. II, pp. 679--696, Colloq. Math. Soc. János Bolyai, 18, North-Holland, Amsterdam-New York, 1978.
*[R] Reed, B.A.,  , and
, and  , J. Graph Theory 27 (1998) 177-212.
, J. Graph Theory 27 (1998) 177-212.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University
Modifying the conjecture
From Reed's conjecture, it seems that the ceiling has to be replaced by flooring. Thanks.