 login/create account
login/create account
Kostochka, Alexandr V.
List Total Colouring Conjecture ★★
Author(s): Borodin; Kostochka; Woodall
Conjecture If 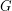 is the total graph of a multigraph, then
is the total graph of a multigraph, then 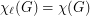 .
.
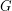 is the total graph of a multigraph, then
is the total graph of a multigraph, then 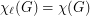 .
. Keywords: list coloring; Total coloring; total graphs
Acyclic list colouring of planar graphs. ★★★
Author(s): Borodin; Fon-Der-Flasss; Kostochka; Raspaud; Sopena
Conjecture Every planar graph is acyclically 5-choosable.
Keywords:
The Borodin-Kostochka Conjecture ★★
Conjecture Every graph with maximum degree 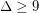 has chromatic number at most
has chromatic number at most 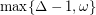 .
.
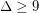 has chromatic number at most
has chromatic number at most 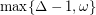 .
. Keywords:
Bounding the chromatic number of triangle-free graphs with fixed maximum degree ★★
Conjecture A triangle-free graph with maximum degree 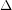 has chromatic number at most
has chromatic number at most 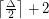 .
.
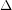 has chromatic number at most
has chromatic number at most 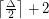 .
.
Keywords: chromatic number; girth; maximum degree; triangle free

 Drupal
Drupal CSI of Charles University
CSI of Charles University