 login/create account
login/create account
Total coloring
List Total Colouring Conjecture ★★
Author(s): Borodin; Kostochka; Woodall
Conjecture If  is the total graph of a multigraph, then
is the total graph of a multigraph, then 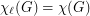 .
.
 is the total graph of a multigraph, then
is the total graph of a multigraph, then 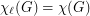 .
. Keywords: list coloring; Total coloring; total graphs
Total Colouring Conjecture ★★★
Author(s): Behzad
Conjecture A total coloring of a graph 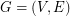 is an assignment of colors to the vertices and the edges of
is an assignment of colors to the vertices and the edges of  such that every pair of adjacent vertices, every pair of adjacent edges and every vertex and incident edge pair, receive different colors. The total chromatic number of a graph
such that every pair of adjacent vertices, every pair of adjacent edges and every vertex and incident edge pair, receive different colors. The total chromatic number of a graph  ,
, 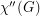 , equals the minimum number of colors needed in a total coloring of
, equals the minimum number of colors needed in a total coloring of  . It is an old conjecture of Behzad that for every graph
. It is an old conjecture of Behzad that for every graph  , the total chromatic number equals the maximum degree of a vertex in
, the total chromatic number equals the maximum degree of a vertex in  ,
, 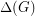 plus one or two. In other words,
plus one or two. In other words, ![\[\chi''(G)=\Delta(G)+1\ \ or \ \ \Delta(G)+2.\]](/files/tex/d4ea30e930ec20e02c5a03c6322e6d99a6bdb63a.png)
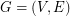 is an assignment of colors to the vertices and the edges of
is an assignment of colors to the vertices and the edges of  such that every pair of adjacent vertices, every pair of adjacent edges and every vertex and incident edge pair, receive different colors. The total chromatic number of a graph
such that every pair of adjacent vertices, every pair of adjacent edges and every vertex and incident edge pair, receive different colors. The total chromatic number of a graph  ,
, 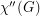 , equals the minimum number of colors needed in a total coloring of
, equals the minimum number of colors needed in a total coloring of  . It is an old conjecture of Behzad that for every graph
. It is an old conjecture of Behzad that for every graph  , the total chromatic number equals the maximum degree of a vertex in
, the total chromatic number equals the maximum degree of a vertex in  ,
, 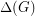 plus one or two. In other words,
plus one or two. In other words, ![\[\chi''(G)=\Delta(G)+1\ \ or \ \ \Delta(G)+2.\]](/files/tex/d4ea30e930ec20e02c5a03c6322e6d99a6bdb63a.png)
Keywords: Total coloring

 Drupal
Drupal CSI of Charles University
CSI of Charles University