 login/create account
login/create account
list coloring
List Colourings of Complete Multipartite Graphs with 2 Big Parts ★★
Author(s): Allagan
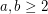 , what is the smallest integer
, what is the smallest integer 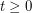 such that
such that 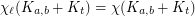 ?
? Keywords: complete bipartite graph; complete multipartite graph; list coloring
List Total Colouring Conjecture ★★
Author(s): Borodin; Kostochka; Woodall
 is the total graph of a multigraph, then
is the total graph of a multigraph, then 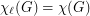 .
. Keywords: list coloring; Total coloring; total graphs
Choosability of Graph Powers ★★
Author(s): Noel
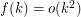 such that for every graph
such that for every graph  ,
, ![\[\text{ch}\left(G^2\right)\leq f\left(\chi\left(G^2\right)\right)?\]](/files/tex/989db06683633e86605c26e7d9f0bffc7e46a496.png)
Keywords: choosability; chromatic number; list coloring; square of a graph
Bounding the on-line choice number in terms of the choice number ★★
Author(s): Zhu
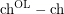 is arbitrarily large?
is arbitrarily large? Keywords: choosability; list coloring; on-line choosability
Choice number of complete multipartite graphs with parts of size 4 ★
Author(s):
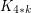 for general
for general  ?
? Keywords: choosability; complete multipartite graph; list coloring
Choice Number of k-Chromatic Graphs of Bounded Order ★★
Author(s): Noel
 is a
is a  -chromatic graph on at most
-chromatic graph on at most 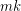 vertices, then
vertices, then 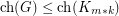 .
. Keywords: choosability; complete multipartite graph; list coloring
Ohba's Conjecture ★★
Author(s): Ohba
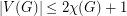 , then
, then 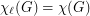 .
. Keywords: choosability; chromatic number; complete multipartite graph; list coloring
Partial List Coloring ★★★
Author(s): Iradmusa
Let  be a simple graph, and for every list assignment
be a simple graph, and for every list assignment 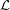 let
let 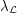 be the maximum number of vertices of
be the maximum number of vertices of  which are colorable with respect to
which are colorable with respect to 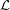 . Define
. Define  , where the minimum is taken over all list assignments
, where the minimum is taken over all list assignments 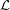 with
with 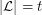 for all
for all 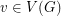 .
.
 be a graph with list chromatic number
be a graph with list chromatic number 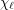 and
and 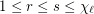 . Then
. Then ![\[\frac{\lambda_r}{r}\geq\frac{\lambda_s}{s}.\]](/files/tex/47be18e956355dd433b88b66eabf01a9e3ed5f61.png)
Keywords: list assignment; list coloring
Partial List Coloring ★★★
Author(s): Albertson; Grossman; Haas
 be a simple graph with
be a simple graph with  vertices and list chromatic number
vertices and list chromatic number 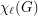 . Suppose that
. Suppose that 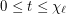 and each vertex of
and each vertex of  is assigned a list of
is assigned a list of  colors. Then at least
colors. Then at least 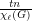 vertices of
vertices of  can be colored from these lists.
can be colored from these lists. Keywords: list assignment; list coloring
List colorings of edge-critical graphs ★★
Author(s): Mohar
 is a
is a  -edge-critical graph. Suppose that for each edge
-edge-critical graph. Suppose that for each edge  of
of  , there is a list
, there is a list 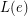 of
of  colors. Then
colors. Then  is
is  -edge-colorable unless all lists are equal to each other.
-edge-colorable unless all lists are equal to each other. Keywords: edge-coloring; list coloring

 Drupal
Drupal CSI of Charles University
CSI of Charles University