Home » Subject » Graph Theory » Coloring » Vertex coloring
Importance: Medium ✭✭
Author(s): Noel, Jonathan A.
Subject: Graph Theory
» Coloring
» » Vertex coloring
Keywords: choosability
chromatic number
list coloring
square of a graph
Recomm. for undergrads: yes
Posted by: Jon Noel
on: July 13th, 2013
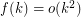Question  (Noel, 2013)   Does there exist a function $ f(k)=o(k^2) $ such that for every graph $ G $, \[\text{ch}\left(G^2\right)\leq f\left(\chi\left(G^2\right)\right)?\]

For a survey of choosability, including relevant definitions, see [Noe] or click here.

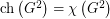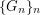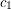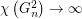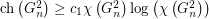The List Square Colouring Conjecture, due to Kostochka and Woodall [KW], states that $ \text{ch}\left(G^2\right) = \chi\left(G^2\right) $ for every graph $ G $. This was disproved by Kim and Park [KP], who proved that there is a sequence $ \{G_n\}_n $ of graphs and a constant $ c_1 $ such that $ \chi\left(G^2_n\right)\to\infty $ and $ \text{ch}\left(G_n^2\right) \geq c_1 \chi\left(G_n^2\right)\log\left(\chi\left(G_n^2\right)\right) $ for all $ n $. To obtain this lower bound from the construction of Kim and Park, one can apply the well-known result of Alon [Alo].

It may be the case that the correct upper bound for all graphs is of the same order of magnitude as the example in the result of Kim and Park.

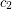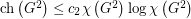Question  (Noel, 2013)   Does there exist a positive constant $ c_2 $ such that every graph $ G $ satisfies $ \text{ch}\left(G^2\right) \leq c_2\chi\left(G^2\right)\log{\chi\left(G^2\right)} $?

By calculating the clique number and maximum degree of 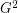$ G^2 $, one can easily show that 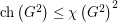$ \text{ch}\left(G^2\right)\leq\chi\left(G^2\right)^2 $ (this observation is due to Young Soo Kwon), but it seems that no significantly better bound is known.

Proposition   If $ G $ contains an edge, then \[\text{ch}\left(G^2\right)< \chi\left(G^2\right)^2.\]
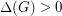Proof   We observe the following bounds: \[\chi\left(G^2\right) \geq \omega\left(G^2\right) \geq \Delta(G)+1,\] \[\text{ch}\left(G^2\right) \leq \Delta\left(G^2\right)+1 \leq \Delta(G)\left(\Delta(G)-1\right) + \Delta(G)+1 = \Delta(G)^2+1.\] Therefore, since $ \Delta(G)>0 $, we have \[\text{ch}\left(G^2\right)\leq \Delta(G)^2+1 < \left(\Delta(G)+1\right)^2 \leq \chi\left(G^2\right)^2.\] This completes the proof.

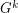These questions are related to a problem of Zhu (see Doug West's webpage for more info) who asked whether there exists an integer $ k $ such that for every graph $ G $, we have that $ G^k $ has choice number equal to chromatic number. This conjecture has been disproved independently by Kim, Kwon and Park [KKP] and Kosar, Petrickova, Reigniger and Yeager [KPRY]. 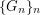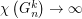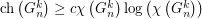The example of [KPRY] also yields, for every $ k $, a sequence $ \{G_n\}_n $ of graphs and a constant $ c $ such that $ \chi\left(G^k_n\right)\to\infty $ and $ \text{ch}\left(G_n^k\right) \geq c \chi\left(G_n^k\right)\log\left(\chi\left(G_n^k\right)\right) $ for all $ n $. They ask the following, more general, questions:

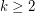Question  (Kosar et al., 2013)   Given $ k\geq2 $, does there exist a function 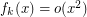$ f_k(x)=o(x^2) $ such that for every graph $ G $, \[\text{ch}\left(G^k\right)\leq f_k\left(\chi\left(G^k\right)\right)?\]

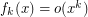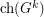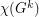To our knowledge, it is not known whether there exists a function $ f_k(x) = o(x^k) $ such that the same conclusion holds. (Intuitively, it seems that higher values of $ k $ should yield a smaller separation between $ \text{ch}(G^k) $ and $ \chi(G^k) $; however, there seems to be no hard evidence to support this.)

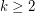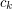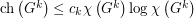Question  (Kosar et al., 2013)   Given $ k\geq2 $, does there exist a positive constant $ c_k $ such that every graph $ G $ satisfies $ \text{ch}\left(G^k\right) \leq c_k\chi\left(G^k\right)\log{\chi\left(G^k\right)} $? Moreover, can the constant 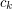$ c_k $ be made independent of $ k $?

These questions are also related to the so-called List Total Colouring Conjecture of Borodin, Kostochka and Woodall [BKW], which says that the total graph of a multigraph always satisfies 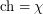$ \text{ch}=\chi $. Given a multigraph $ G $, the total graph of $ G $ can be obtained by subdividing every edge of $ G $ and then taking the square of the resulting graph.

Related problems

Choice number of complete multipartite graphs with parts of size 4
Choice Number of k-Chromatic Graphs of Bounded Order
List Total Colouring Conjecture

Bibliography

[Alo] Noga Alon. Choice numbers of graphs: a probabilistic approach. Combin. Probab. Comput., 1(2):107–114, 1992.

[BKW] Oleg V. Borodin, Alexandr V. Kostochka, and Douglas R. Woodall. List edge and list total colourings of multigraphs. J. Combin. Theory Ser. B, 71(2):184–204, 1997.

[KP] Seog-Jin Kim and Boram Park: Counterexamples to the List Square Coloring Conjecture, submitted.

[KKP] Seog-Jin Kim, Young Soo Kwon and Boram Park: Chromatic-choosability of the power of graphs.

[KPRY] Nicholas Kosar, Sarka Petrickova, Benjamin Reiniger, Elyse Yeager: A note on list-coloring powers of graphs.

[KW] Alexandr V. Kostochka and Douglas R. Woodall. Choosability conjectures and multicircuits, Discrete Math., 240 (2001), 123--143.

[Noe] Jonathan A. Noel. Choosability of Graphs with Bounded Order: Ohba's Conjecture and Beyond, Master's thesis. McGill University (2013). pdf.


* indicates original appearance(s) of problem.
add new comment

Reply

Comments are limited to a maximum of 1000 characters.
More information about formatting options