 login/create account
login/create account
Iradmusa, Moharram
Vertex Coloring of graph fractional powers ★★★
Author(s): Iradmusa
Conjecture Let  be a graph and
be a graph and  be a positive integer. The
be a positive integer. The 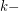 power of
power of  , denoted by
, denoted by 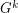 , is defined on the vertex set
, is defined on the vertex set 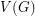 , by connecting any two distinct vertices
, by connecting any two distinct vertices  and
and 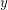 with distance at most
with distance at most  . In other words,
. In other words, 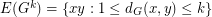 . Also
. Also 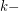 subdivision of
subdivision of  , denoted by
, denoted by 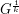 , is constructed by replacing each edge
, is constructed by replacing each edge 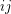 of
of  with a path of length
with a path of length  . Note that for
. Note that for 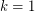 , we have
, we have 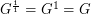 .
.
Now we can define the fractional power of a graph as follows:
Let be a graph and
be a graph and 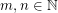 . The graph
. The graph 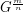 is defined by the
is defined by the 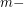 power of the
power of the 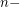 subdivision of
subdivision of  . In other words
. In other words 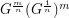 .
.
Conjecture. Let be a connected graph with
be a connected graph with 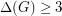 and
and  be a positive integer greater than 1. Then for any positive integer
be a positive integer greater than 1. Then for any positive integer 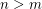 , we have
, we have 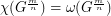 .
.
In [1], it was shown that this conjecture is true in some special cases.
 be a graph and
be a graph and  be a positive integer. The
be a positive integer. The 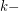 power of
power of  , denoted by
, denoted by 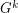 , is defined on the vertex set
, is defined on the vertex set 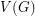 , by connecting any two distinct vertices
, by connecting any two distinct vertices  and
and 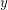 with distance at most
with distance at most  . In other words,
. In other words, 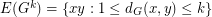 . Also
. Also 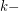 subdivision of
subdivision of  , denoted by
, denoted by 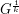 , is constructed by replacing each edge
, is constructed by replacing each edge 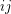 of
of  with a path of length
with a path of length  . Note that for
. Note that for 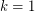 , we have
, we have 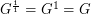 .
.Now we can define the fractional power of a graph as follows:
Let
 be a graph and
be a graph and 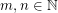 . The graph
. The graph 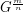 is defined by the
is defined by the 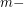 power of the
power of the 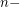 subdivision of
subdivision of  . In other words
. In other words 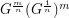 .
.Conjecture. Let
 be a connected graph with
be a connected graph with 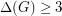 and
and  be a positive integer greater than 1. Then for any positive integer
be a positive integer greater than 1. Then for any positive integer 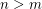 , we have
, we have 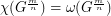 .
.In [1], it was shown that this conjecture is true in some special cases.
Keywords: chromatic number, fractional power of graph, clique number
Partial List Coloring ★★★
Author(s): Iradmusa
Let  be a simple graph, and for every list assignment
be a simple graph, and for every list assignment 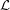 let
let 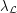 be the maximum number of vertices of
be the maximum number of vertices of  which are colorable with respect to
which are colorable with respect to 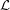 . Define
. Define  , where the minimum is taken over all list assignments
, where the minimum is taken over all list assignments 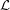 with
with 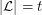 for all
for all 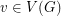 .
.
Conjecture [2] Let  be a graph with list chromatic number
be a graph with list chromatic number 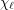 and
and 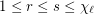 . Then
. Then ![\[\frac{\lambda_r}{r}\geq\frac{\lambda_s}{s}.\]](/files/tex/47be18e956355dd433b88b66eabf01a9e3ed5f61.png)
 be a graph with list chromatic number
be a graph with list chromatic number 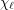 and
and 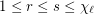 . Then
. Then ![\[\frac{\lambda_r}{r}\geq\frac{\lambda_s}{s}.\]](/files/tex/47be18e956355dd433b88b66eabf01a9e3ed5f61.png)
Keywords: list assignment; list coloring

 Drupal
Drupal CSI of Charles University
CSI of Charles University