 login/create account
login/create account
Ohba's Conjecture (Solved)
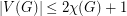 , then
, then 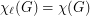 .
. Basics of List Colouring
A  -list assignment of a graph
-list assignment of a graph  is an assignment of lists
is an assignment of lists 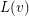 of
of  `available colours' to the vertices of
`available colours' to the vertices of  . A graph is said to be
. A graph is said to be 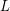 -choosable if it can be properly coloured from the prescribed lists, and
-choosable if it can be properly coloured from the prescribed lists, and  -choosable if this property holds for every
-choosable if this property holds for every  -list assignment.
-list assignment.
 , we define the list chromatic number of
, we define the list chromatic number of  by
by 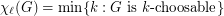 .
. The lower bound 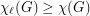 is easily observed by assigning the same list to every vertex. However, the reverse inequality does not hold in general. In their classic paper [4], Erdos, Rubin and Taylor give the example of
is easily observed by assigning the same list to every vertex. However, the reverse inequality does not hold in general. In their classic paper [4], Erdos, Rubin and Taylor give the example of 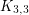 where the three vertices on either side of the bipartition are given lists
where the three vertices on either side of the bipartition are given lists 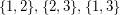 . One may check that no list colouring exists despite the fact that all lists have size two. Note that this example shows that the conjecture, if true, would be tight.
. One may check that no list colouring exists despite the fact that all lists have size two. Note that this example shows that the conjecture, if true, would be tight.
In general, there are bipartite graphs with arbitrarily high list chromatic number and so 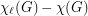 can be arbitrarily large. A natural question arises: What conditions guarantee that
can be arbitrarily large. A natural question arises: What conditions guarantee that 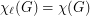 ? A graph
? A graph  with this property is said to be chromatic-choosable.
with this property is said to be chromatic-choosable.
The Conjecture
Erdos, Rubin and Taylor proved that every multipartite graph with all parts of size two is chromatic-choosable [4]. In [12] Gravier and Maffray show that the propertiy still holds if one of the parts has size three. Ohba's Conjecture [1] above can be seen as a generalization. Some weaker versions have been proven:
 ] If
] If 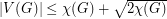 , then
, then  is chromatic-choosable.
is chromatic-choosable. 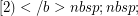 ] If
] If 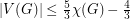 , then
, then  is chromatic-choosable.
is chromatic-choosable. 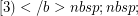 ] If
] If 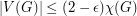 where
where 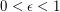 and
and 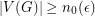 , then
, then  is chromatic-choosable.
is chromatic-choosable. One may observe that Ohba's conjecture holds for all graphs if and only if it holds for complete multipartite graphs. Indeed, given a counterexample we may add an edge between vertices of different colour classes to yeilds another counterexample. Thus, the main focus of [6-11] has been on verifying Ohba's conjecture for certain classes of multipartite graphs. It is now known that complete multipartite graphs having parts of size 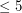 satisfy Ohba's conjecture [11]. In other words, the conjecture is solved for graphs with independance number at most five.
satisfy Ohba's conjecture [11]. In other words, the conjecture is solved for graphs with independance number at most five.
Ohba's Conjecture can be found as unsolved problem #50 in Bondy and Murty's book "Graph Theory" [15].
The problem was recently solved [13]. The proof can be found here. It can also be found here. Click here for a problem which generalizes Ohba's Conjecture.
Bibliography
*[1] K. Ohba. On chromatic-choosable graphs, J. Graph Theory. 40 (2002) 130--135. MathSciNet.
[2] B. Reed, B. Sudakov. List colouring when the chromatic number is close to the order of the graph, Combinatorica 25 (1) (2004) 117--123. MathSciNet.
[3] B. Reed, B. Sudakov. List colouring of graphs with at most 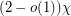 vertices, Beijing, 2002, in: Proceedings of the International Congress of Mathematicians, vol. III, Higher Ed. Press, Beijing (2002) 587–-603.
vertices, Beijing, 2002, in: Proceedings of the International Congress of Mathematicians, vol. III, Higher Ed. Press, Beijing (2002) 587–-603.
[4] P. Erdős, A. L. Rubin, H. Taylor, Choosability in graphs, Proc. West Coast Conference on Combinatorics, Graph Theory and Computing, Arcata, Congressus Numerantium 26 (1979) 125–-157. pdf.
[6] H. Enomoto, K. Ohba, K. Ota, J. Sakamoto. Choice number of some complete multi-partite graphs, Discrete Math. 244 (1-3) (2002) 55--66.
[7] K. Ohba. Choice number of complete multipartite graphs with part size at most three, Ars Combin. 72 (2004) 133--139.
[8] Y. Shen, W. He, G. Zheng, Y. Wang, L. Zhang. On choosability of some complete multipartite graphs and Ohba's conjecture, Discrete Math. 308 (1) (2008) 136--143.
[9] W. He, L. Zhang, D. W. Cranston, Y. Shen, G. Zheng. Choice number of complete multipartite graphs 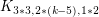 and
and 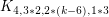 , Discrete Math. 308 (23) (2008) 5871–-5877.
, Discrete Math. 308 (23) (2008) 5871–-5877.
[10] G. Zheng, Y. Shen, Z. Chen, J. Lv. On choosability of complete multipartite graphs 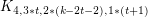 , Discuss. Math. Graph Theory 30 (2) (2010) 237–-244.
, Discuss. Math. Graph Theory 30 (2) (2010) 237–-244.
[11] A. V. Kostochka, M. Stiebitz, D. R. Woodall. Ohba's conjecture for graphs with independence number five, Discrete Math. 311 (12) (2011) 996--1005. ScienceDirect.
[12] S. Gravier, F. Maffray. Graphs whose choice number is equal to their chromatic number, J. Graph Theory 27 (1998) 87--97. MathSciNet.
[13] J. A. Noel, B. A. Reed, H. Wu. A Proof of a Conjecture of Ohba. Submitted. pdf.
[14] J. A. Noel. Choosability of Graphs with Bounded Order: Ohba's Conjecture and Beyond. Master's Thesis, McGill University. pdf.
[15] J. A. Bondy and U. S. R. Murty. Graph theory, volume 244 of Graduate Texts in Mathematics. Springer, New York, 2008.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University