 login/create account
login/create account
The Borodin-Kostochka Conjecture
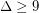 has chromatic number at most
has chromatic number at most 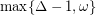 .
.
The Borodin-Kostochka conjecture proposes that for any graph  with maximum degree
with maximum degree  and clique number
and clique number  ,
,  is
is 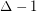 colourable so long as
colourable so long as  is sufficiently large (specifically,
is sufficiently large (specifically, 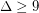 ). The requirement that
). The requirement that 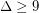 is necessary, as one can see by looking at the strong product of
is necessary, as one can see by looking at the strong product of 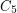 and
and 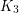 .
.
Reed [R] proved that there exists a 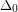 for which the conjecture holds whenever
for which the conjecture holds whenever 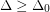 . Specifically he proved that
. Specifically he proved that 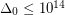 , but claims that more careful analysis could reduce
, but claims that more careful analysis could reduce 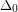 to 1000.
to 1000.
The conjecture was recently proven by Cranston and Rabern for claw-free graphs [CR]. In their paper they mention an unpublished strengthening proposed by Borodin and Kostochka, namely that one can replace the chromatic number in the statement of the conjecture with the list chromatic number.
Bibliography
[BK] O. V. Borodin and A. V. Kostochka. On an upper bound of a graph's chromatic number, depending on the graph's degree and density. JCTB 23 (1977), 247--250.
[CR] D. W. Cranston and L. Rabern. Coloring claw-free graphs with 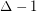 colors, arXiv 1206.1269, 2012.
colors, arXiv 1206.1269, 2012.
[R] B. A. Reed. A strengthening of Brooks’ Theorem. J. Comb. Theory Ser. B, 76:136–149, 1999.
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University