Grunbaum's Conjecture

Importance: High ✭✭✭

Author(s):

Subject:	Graph Theory
	» Topological Graph Theory
	» » Coloring

Keywords:	coloring
	surface

Recomm. for undergrads: no

Posted	by:	mdevos
	on:	April 4th, 2007

Conjecture If $G$ is a simple loopless triangulation of an orientable surface, then the dual of $G$ is 3-edge-colorable.

The Four Color Theorem is equivalent to the statement that every cubic planar graph with no bridge is 3-edge-colorable. This is precisely equivalent to Grunbaum's conjecture restricted to the plane. Thus, Grunbaum's conjecture, if true, would imply the Four Color Theorem. Indeed, this conjecture suggests a deep generalization of the 4-color theorem.

Definition: A cubic graph $G$ is a snark if $G$ is internally 4-edge-connected and $G$ is not 3-edge-colorable.

Grunbaum's conjecture states that no snark is the dual of a simple loopless triangulation of an orientable surface. In this light, the conjecture looks to be almost obviously false. To find a counterexample, it suffices to embed a snark in an orientable surface so that the dual has no loops or parallel edges. Of course, the difficulty is in satisfying this last constraint. All known embeddings of snarks in orientable surfaces give rise to either loops or parallel edges in the dual. It is striking to compare this conjecture with the Orientable cycle double cover conjecture. Both conjectures may be stated in terms of embedding snarks in orientable surfaces as follows:

Conjecture (Grunbaum's conjecture (version 2)) Every embedding of a snark in an orientable surface has a cycle of length 1 or 2 (a loop or parallel edges) in the dual.

Conjecture (Orientable cycle double cover conjecture) Every snark may be embedded in an orientable surface so that the dual graph has no cycle of length 1 (no loop).

In this light it may look unlikely that both Grunbaum's conjecture and the orientable cycle double cover conjecture are true. I (M. DeVos) don't have a strong sense for or against either of these conjectures, and I don't believe there is a strong consensus among experts.

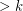Mohar and Robertson have suggested the following weak version of Grunbaum's conjecture: There exists a fixed constant $k$ so that the dual of every loopless triangulation of an orientable surface of face-width $>k$ is 3-edge-colorable. Robertson has suggested that this may still hold true even for nonorientable surfaces. The following conjecture is a further weakening of Grunbaum's conjecture which would allow the parameter $k$ to depend on the surface. This is probably the weakest open problem in this vein.

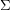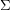Conjecture (Weak Grunbaum conjecture) For every orientable surface $\Sigma$ , there is a fixed constant $k$ so that the dual of every loopless triangulation of $\Sigma$ with face-width 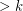$>k$ is 3-edge-colorable.

Bibliography

[G] B. Grunbaum, Conjecture 6. In Recent progress in combinatorics, (W.T. Tutte Ed.), Academic Press (1969) 343.

* indicates original appearance(s) of problem.

add new comment

Grunbaum's conjecture is false!

On October 4th, 2007 Anonymous says:

Martin Kochol and Bojan Mohar announced a counterexample to Grunbaum's conjecture at the PIMS Workshop on the Cycle Double Cover Conjecture (Vancouver, 2007). By using Kochol's "superposition" operation on several copies of Petersen's graph, they constructed a snark which embeds on the orientable surface of genus 9, and whose dual contains no loops or parallel edges.

Of course Grunbaum's Conjecture may still hold true for lower-genus surfaces, in particular, the torus.

Ref: Kochol, M; Mohar, B; preprint 2007.

Solution

On March 23rd, 2009 Anonymous says:

The solution of the Grunbaum's conjecture is published in (see also http://www.mat.savba.sk/~kochol):

M. Kochol, 3-Regular non 3-edge-colorable graphs with polyhedral embeddings in orientable surfaces, in: Graph Drawing 2008, Editors: I.G. Tollis, M. Patrignani, Lecture Notes in Computer Science, Vol. 5417, Springer-Verlag, Berlin, 2009, pp. 319-323

M. Kochol, Polyhedral embeddings of snarks in orientable surfaces, Proceedings of the American Mathematical Society vol. 137 (2009), pp. 1613-1619.

Wrong information. Martin

On November 25th, 2007 Anonymous says:

Wrong information. Martin Kochol

so ?

On December 17th, 2007 Anonymous says:

Sorry I don't understand, is the conjecture false or still opened ?

False in general

On December 19th, 2007 Anonymous says:

A counter example was found on the nine holed torus, and I have heard there is now one on the five holed torus as well so the conjecture is false in general. However what is still not known is for which n does the conjecture hold for the n-holed torus, and in particular the one holed torus is always of interest and remains open.

Open Problem Garden