 login/create account
login/create account
surface
5-local-tensions ★★
Author(s): DeVos
Conjecture There exists a fixed constant  (probably
(probably 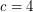 suffices) so that every embedded (loopless) graph with edge-width
suffices) so that every embedded (loopless) graph with edge-width 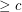 has a 5-local-tension.
has a 5-local-tension.
 (probably
(probably 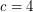 suffices) so that every embedded (loopless) graph with edge-width
suffices) so that every embedded (loopless) graph with edge-width 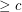 has a 5-local-tension.
has a 5-local-tension. Drawing disconnected graphs on surfaces ★★
Author(s): DeVos; Mohar; Samal
Conjecture Let  be the disjoint union of the graphs
be the disjoint union of the graphs 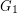 and
and 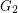 and let
and let 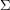 be a surface. Is it true that every optimal drawing of
be a surface. Is it true that every optimal drawing of  on
on  has the property that
has the property that 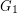 and
and 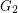 are disjoint?
are disjoint?
 be the disjoint union of the graphs
be the disjoint union of the graphs 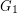 and
and 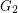 and let
and let 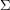 be a surface. Is it true that every optimal drawing of
be a surface. Is it true that every optimal drawing of  on
on 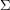 has the property that
has the property that 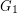 and
and 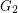 are disjoint?
are disjoint? Keywords: crossing number; surface
Grunbaum's Conjecture ★★★
Author(s): Grunbaum
Conjecture If  is a simple loopless triangulation of an orientable surface, then the dual of
is a simple loopless triangulation of an orientable surface, then the dual of  is 3-edge-colorable.
is 3-edge-colorable.
 is a simple loopless triangulation of an orientable surface, then the dual of
is a simple loopless triangulation of an orientable surface, then the dual of  is 3-edge-colorable.
is 3-edge-colorable. Consecutive non-orientable embedding obstructions ★★★
Author(s):
Conjecture Is there a graph  that is a minor-minimal obstruction for two non-orientable surfaces?
that is a minor-minimal obstruction for two non-orientable surfaces?
 that is a minor-minimal obstruction for two non-orientable surfaces?
that is a minor-minimal obstruction for two non-orientable surfaces? 
 Drupal
Drupal CSI of Charles University
CSI of Charles University