 login/create account
login/create account
5-local-tensions
 (probably
(probably 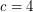 suffices) so that every embedded (loopless) graph with edge-width
suffices) so that every embedded (loopless) graph with edge-width 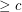 has a 5-local-tension.
has a 5-local-tension. The edge-width of an embedded graph is the length of the shortest non-contractible cycle.
 be a directed graph, let
be a directed graph, let 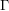 be an abelian group, and let
be an abelian group, and let 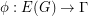 . Define the height of a walk
. Define the height of a walk 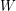 to be the sum of
to be the sum of 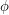 on the forward edges of
on the forward edges of 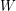 minus the sum of
minus the sum of 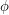 on the backward edges of
on the backward edges of 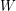 (edges are counted according to multiplicity). We call
(edges are counted according to multiplicity). We call 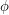 a tension if the height of every closed walk is zero, and if
a tension if the height of every closed walk is zero, and if  is an embedded graph, we call
is an embedded graph, we call 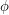 a local-tension if the height of every closed walk which forms a contractible curve is zero. If in addition,
a local-tension if the height of every closed walk which forms a contractible curve is zero. If in addition, 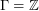 and
and 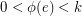 for some
for some 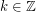 , we say that
, we say that 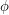 is a
is a  -tension or a
-tension or a  -local-tension. If we reverse an edge
-local-tension. If we reverse an edge  and replace
and replace 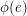 by
by 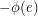 , this preserves the properties of tension or local-tension. Accordingly, we say that an undirected graph (embedded graph)
, this preserves the properties of tension or local-tension. Accordingly, we say that an undirected graph (embedded graph)  has a
has a  -tension (
-tension ( -local-tension) if some and thus every orientation of it admits such a map.
-local-tension) if some and thus every orientation of it admits such a map.  -tension if and only if it is
-tension if and only if it is  -colorable.
-colorable. 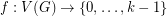 be a coloring, orient the edges of
be a coloring, orient the edges of  arbitrarily, and defining
arbitrarily, and defining 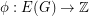 by the rule
by the rule 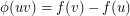 . It is straightforward to check that
. It is straightforward to check that 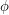 is a
is a  -tension. For the "only if" direction, let
-tension. For the "only if" direction, let 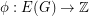 be a
be a  -tension. Now choose a point
-tension. Now choose a point 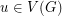 and define the map
and define the map 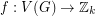 by the rule that
by the rule that 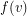 is the height of some (and thus every) walk from
is the height of some (and thus every) walk from  to
to  modulo
modulo  . Again, it is straightforward to check that this defines a proper
. Again, it is straightforward to check that this defines a proper  -coloring.
-coloring. For graphs on orientable surfaces, local-tensions are dual to flows. More precisely, if  and
and 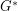 are dual graphs embedded in an orientable surface, then
are dual graphs embedded in an orientable surface, then  has a
has a  -local-tension if and only if
-local-tension if and only if 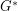 has a nowhere-zero
has a nowhere-zero  -flow. On non-orientable surfaces, there is a duality between
-flow. On non-orientable surfaces, there is a duality between  -local-tensions in
-local-tensions in  and nowhere-zero
and nowhere-zero  -flows in a bidirected
-flows in a bidirected 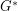 . Based on this duality we have a couple of conjectures. The first follows from Tutte's 5-flow conjecture, the second from Bouchet's 6-flow conjecture.
. Based on this duality we have a couple of conjectures. The first follows from Tutte's 5-flow conjecture, the second from Bouchet's 6-flow conjecture.
So although, graphs on surfaces may have high chromatic number, thanks to some partial results toward the above conjectures, we know that they always have small local-tensions. For orientable surfaces, there is a famous Conjecture of Grunbaum which is equivalent to the following.
 is a simple loopless graph embedded in an orientable surface with edge-width
is a simple loopless graph embedded in an orientable surface with edge-width 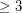 , then
, then  has a 4-local-tension.
has a 4-local-tension. On non-orientable surfaces, it is known that there are graphs of arbitrarily high edge-width which do not admit 4-local-tensions (see [DGMVZ]). However, it remains open whether sufficiently high edge-width forces the existence of a 5-local-tension. Indeed, as suggested by the conjecture at the start of this page, it may be that edge-width at least 4 is enough. Edge-width 3 does not suffice since the embedding of 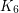 in the projective plane does not admit a 5-local-tension.
in the projective plane does not admit a 5-local-tension.
Bibliography
*[DGMVZ] M. DeVos, L. Goddyn, B. Mohar, D. Vertigan, and X. Zhu, Coloring-flow duality of embedded graphs. Trans. Amer. Math. Soc. 357 (2005), no. 10 MathSciNet
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University