 login/create account
login/create account
DeVos, Matt
Friendly partitions ★★
Author(s): DeVos
A friendly partition of a graph is a partition of the vertices into two sets so that every vertex has at least as many neighbours in its own class as in the other.
 , all but finitely many
, all but finitely many  -regular graphs have friendly partitions?
-regular graphs have friendly partitions? Circular colouring the orthogonality graph ★★
Author(s): DeVos; Ghebleh; Goddyn; Mohar; Naserasr
Let  denote the graph with vertex set consisting of all lines through the origin in
denote the graph with vertex set consisting of all lines through the origin in 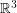 and two vertices adjacent in
and two vertices adjacent in  if they are perpendicular.
if they are perpendicular.
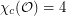 ?
? Keywords: circular coloring; geometric graph; orthogonality
5-local-tensions ★★
Author(s): DeVos
 (probably
(probably 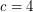 suffices) so that every embedded (loopless) graph with edge-width
suffices) so that every embedded (loopless) graph with edge-width 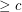 has a 5-local-tension.
has a 5-local-tension. Gao's theorem for nonabelian groups ★★
Author(s): DeVos
For every finite multiplicative group  , let
, let 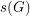 (
(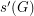 ) denote the smallest integer
) denote the smallest integer  so that every sequence of
so that every sequence of  elements of
elements of  has a subsequence of length
has a subsequence of length  (length
(length 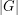 ) which has product equal to 1 in some order.
) which has product equal to 1 in some order.
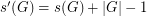 for every finite group
for every finite group  .
. Keywords: subsequence sum; zero sum
Antichains in the cycle continuous order ★★
Author(s): DeVos
If  ,
, are graphs, a function
are graphs, a function 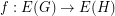 is called cycle-continuous if the pre-image of every element of the (binary) cycle space of
is called cycle-continuous if the pre-image of every element of the (binary) cycle space of  is a member of the cycle space of
is a member of the cycle space of  .
.
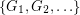 so that there is no cycle continuous mapping between
so that there is no cycle continuous mapping between 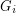 and
and 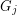 whenever
whenever 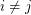 ?
? Drawing disconnected graphs on surfaces ★★
Author(s): DeVos; Mohar; Samal
 be the disjoint union of the graphs
be the disjoint union of the graphs 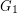 and
and 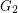 and let
and let 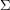 be a surface. Is it true that every optimal drawing of
be a surface. Is it true that every optimal drawing of  on
on 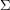 has the property that
has the property that 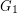 and
and 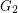 are disjoint?
are disjoint? Keywords: crossing number; surface
What is the largest graph of positive curvature? ★
Keywords: curvature; planar graph
Partitioning edge-connectivity ★★
Author(s): DeVos
 be an
be an 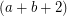 -edge-connected graph. Does there exist a partition
-edge-connected graph. Does there exist a partition 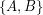 of
of 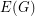 so that
so that 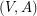 is
is  -edge-connected and
-edge-connected and 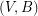 is
is  -edge-connected?
-edge-connected? Keywords: edge-coloring; edge-connectivity
Packing T-joins ★★
Author(s): DeVos
 (probably
(probably 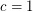 suffices) so that every graft with minimum
suffices) so that every graft with minimum  -cut size at least
-cut size at least  contains a
contains a  -join packing of size at least
-join packing of size at least 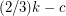 .
. A homomorphism problem for flows ★★
Author(s): DeVos
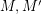 be abelian groups and let
be abelian groups and let 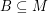 and
and 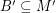 satisfy
satisfy 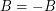 and
and 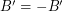 . If there is a homomorphism from
. If there is a homomorphism from 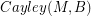 to
to 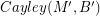 , then every graph with a B-flow has a B'-flow.
, then every graph with a B-flow has a B'-flow. Keywords: homomorphism; nowhere-zero flow; tension

 Drupal
Drupal CSI of Charles University
CSI of Charles University