 login/create account
login/create account
circular coloring
Circular colouring the orthogonality graph ★★
Author(s): DeVos; Ghebleh; Goddyn; Mohar; Naserasr
Let  denote the graph with vertex set consisting of all lines through the origin in
denote the graph with vertex set consisting of all lines through the origin in 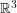 and two vertices adjacent in
and two vertices adjacent in  if they are perpendicular.
if they are perpendicular.
Problem Is 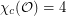 ?
?
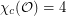 ?
? Keywords: circular coloring; geometric graph; orthogonality
Circular coloring triangle-free subcubic planar graphs ★★
Problem Does every triangle-free planar graph of maximum degree three have circular chromatic number at most 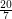 ?
?
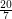 ?
? Keywords: circular coloring; planar graph; triangle free

 Drupal
Drupal CSI of Charles University
CSI of Charles University