 login/create account
login/create account
Goddyn, Luis A.
Circular colouring the orthogonality graph ★★
Author(s): DeVos; Ghebleh; Goddyn; Mohar; Naserasr
Let  denote the graph with vertex set consisting of all lines through the origin in
denote the graph with vertex set consisting of all lines through the origin in 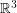 and two vertices adjacent in
and two vertices adjacent in  if they are perpendicular.
if they are perpendicular.
Problem Is 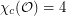 ?
?
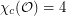 ?
? Keywords: circular coloring; geometric graph; orthogonality
A conjecture on iterated circumcentres ★★
Author(s): Goddyn
Conjecture Let 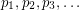 be a sequence of points in
be a sequence of points in 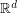 with the property that for every
with the property that for every 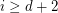 , the points
, the points 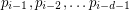 are distinct, lie on a unique sphere, and further,
are distinct, lie on a unique sphere, and further, 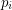 is the center of this sphere. If this sequence is periodic, must its period be
is the center of this sphere. If this sequence is periodic, must its period be 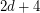 ?
?
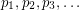 be a sequence of points in
be a sequence of points in 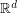 with the property that for every
with the property that for every 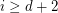 , the points
, the points 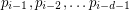 are distinct, lie on a unique sphere, and further,
are distinct, lie on a unique sphere, and further, 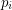 is the center of this sphere. If this sequence is periodic, must its period be
is the center of this sphere. If this sequence is periodic, must its period be 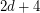 ?
? Keywords: periodic; plane geometry; sequence

 there exists an integer
there exists an integer  so that every
so that every 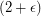 -flow.
-flow.  Drupal
Drupal CSI of Charles University
CSI of Charles University