 login/create account
login/create account
periodic
A conjecture on iterated circumcentres ★★
Author(s): Goddyn
Conjecture Let 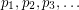 be a sequence of points in
be a sequence of points in 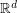 with the property that for every
with the property that for every 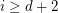 , the points
, the points 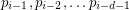 are distinct, lie on a unique sphere, and further,
are distinct, lie on a unique sphere, and further, 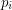 is the center of this sphere. If this sequence is periodic, must its period be
is the center of this sphere. If this sequence is periodic, must its period be 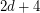 ?
?
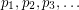 be a sequence of points in
be a sequence of points in 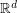 with the property that for every
with the property that for every 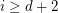 , the points
, the points 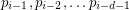 are distinct, lie on a unique sphere, and further,
are distinct, lie on a unique sphere, and further, 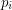 is the center of this sphere. If this sequence is periodic, must its period be
is the center of this sphere. If this sequence is periodic, must its period be 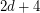 ?
? Keywords: periodic; plane geometry; sequence

 Drupal
Drupal CSI of Charles University
CSI of Charles University