 login/create account
login/create account
A conjecture on iterated circumcentres
Conjecture Let 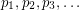 be a sequence of points in
be a sequence of points in 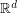 with the property that for every
with the property that for every 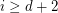 , the points
, the points 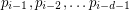 are distinct, lie on a unique sphere, and further,
are distinct, lie on a unique sphere, and further, 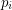 is the center of this sphere. If this sequence is periodic, must its period be
is the center of this sphere. If this sequence is periodic, must its period be 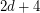 ?
?
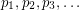 be a sequence of points in
be a sequence of points in 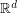 with the property that for every
with the property that for every 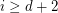 , the points
, the points 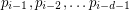 are distinct, lie on a unique sphere, and further,
are distinct, lie on a unique sphere, and further, 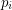 is the center of this sphere. If this sequence is periodic, must its period be
is the center of this sphere. If this sequence is periodic, must its period be 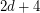 ?
? Luis Goddyn discovered this curiosity, and proved the above conjecture for 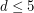 . He also studied related sequences, for instance, the sequence in
. He also studied related sequences, for instance, the sequence in 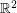 where the
where the 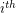 point is the circumcentre of the points with index
point is the circumcentre of the points with index 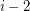 ,
, 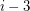 , and
, and 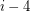 . See Iterated Circumcenters for a delightful and interactive discussion of this problem.
. See Iterated Circumcenters for a delightful and interactive discussion of this problem.
Bibliography
*[G] Luis Goddyn, Iterated Circumcenters
* indicates original appearance(s) of problem.

 Drupal
Drupal CSI of Charles University
CSI of Charles University