 login/create account
login/create account
edge-connectivity
Kriesell's Conjecture ★★
Author(s): Kriesell
Conjecture Let  be a graph and let
be a graph and let 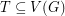 such that for any pair
such that for any pair 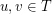 there are
there are 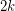 edge-disjoint paths from
edge-disjoint paths from  to
to  in
in  . Then
. Then  contains
contains  edge-disjoint trees, each of which contains
edge-disjoint trees, each of which contains  .
.
 be a graph and let
be a graph and let 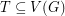 such that for any pair
such that for any pair 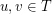 there are
there are 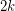 edge-disjoint paths from
edge-disjoint paths from  to
to  in
in  . Then
. Then  contains
contains  edge-disjoint trees, each of which contains
edge-disjoint trees, each of which contains  .
. Keywords: Disjoint paths; edge-connectivity; spanning trees
Partitioning edge-connectivity ★★
Author(s): DeVos
Question Let  be an
be an 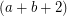 -edge-connected graph. Does there exist a partition
-edge-connected graph. Does there exist a partition 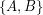 of
of 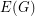 so that
so that 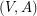 is
is  -edge-connected and
-edge-connected and 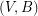 is
is  -edge-connected?
-edge-connected?
 be an
be an 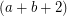 -edge-connected graph. Does there exist a partition
-edge-connected graph. Does there exist a partition 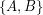 of
of 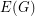 so that
so that 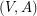 is
is  -edge-connected and
-edge-connected and 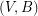 is
is  -edge-connected?
-edge-connected? Keywords: edge-coloring; edge-connectivity

 there exists an integer
there exists an integer 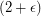 -flow.
-flow.  Drupal
Drupal CSI of Charles University
CSI of Charles University