 login/create account
login/create account
Disjoint paths
Kriesell's Conjecture ★★
Author(s): Kriesell
Conjecture Let  be a graph and let
be a graph and let 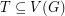 such that for any pair
such that for any pair 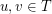 there are
there are 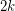 edge-disjoint paths from
edge-disjoint paths from  to
to  in
in  . Then
. Then  contains
contains  edge-disjoint trees, each of which contains
edge-disjoint trees, each of which contains 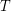 .
.
 be a graph and let
be a graph and let 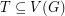 such that for any pair
such that for any pair 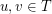 there are
there are 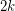 edge-disjoint paths from
edge-disjoint paths from  to
to  in
in  . Then
. Then  contains
contains  edge-disjoint trees, each of which contains
edge-disjoint trees, each of which contains 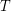 .
. Keywords: Disjoint paths; edge-connectivity; spanning trees
Approximation Ratio for Maximum Edge Disjoint Paths problem ★★
Author(s): Bentz
Conjecture Can the approximation ratio 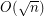 be improved for the Maximum Edge Disjoint Paths problem (MaxEDP) in planar graphs or can an inapproximability result stronger than
be improved for the Maximum Edge Disjoint Paths problem (MaxEDP) in planar graphs or can an inapproximability result stronger than 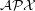 -hardness?
-hardness?
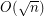 be improved for the Maximum Edge Disjoint Paths problem (MaxEDP) in planar graphs or can an inapproximability result stronger than
be improved for the Maximum Edge Disjoint Paths problem (MaxEDP) in planar graphs or can an inapproximability result stronger than 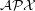 -hardness?
-hardness? Keywords: approximation algorithms; Disjoint paths; planar graph; polynomial algorithm

 Drupal
Drupal CSI of Charles University
CSI of Charles University