 login/create account
login/create account
spanning trees
Kriesell's Conjecture ★★
Author(s): Kriesell
 be a graph and let
be a graph and let 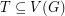 such that for any pair
such that for any pair 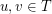 there are
there are 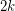 edge-disjoint paths from
edge-disjoint paths from  to
to  in
in  . Then
. Then  contains
contains  edge-disjoint trees, each of which contains
edge-disjoint trees, each of which contains 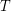 .
. Keywords: Disjoint paths; edge-connectivity; spanning trees
spanning trees ★★
Author(s):
 be a graph with the minimum vertex degree at least 2; that is,
be a graph with the minimum vertex degree at least 2; that is, 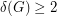 . Then there exists a spanning tree
. Then there exists a spanning tree 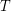 of
of  such that for every support vertex
such that for every support vertex  in
in 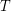 if
if 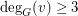 , then
, then 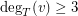 .
. Keywords: spanning trees
What is the smallest number of disjoint spanning trees made a graph Hamiltonian ★★
Author(s): Goldengorin
We are given a complete simple undirected weighted graph 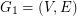 and its first arbitrary shortest spanning tree
and its first arbitrary shortest spanning tree 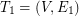 . We define the next graph
. We define the next graph 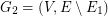 and find on
and find on 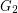 the second arbitrary shortest spanning tree
the second arbitrary shortest spanning tree 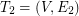 . We continue similarly by finding
. We continue similarly by finding 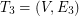 on
on 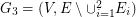 , etc. Let k be the smallest number of disjoint shortest spanning trees as defined above and let
, etc. Let k be the smallest number of disjoint shortest spanning trees as defined above and let 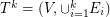 be the graph obtained as union of all
be the graph obtained as union of all  disjoint trees.
disjoint trees.
Question 1. What is the smallest number of disjoint spanning trees creates a graph 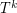 containing a Hamiltonian path.
containing a Hamiltonian path.
Question 2. What is the smallest number of disjoint spanning trees creates a graph 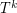 containing a shortest Hamiltonian path?
containing a shortest Hamiltonian path?
Questions 3 and 4. Replace in questions 1 and 2 a shortest spanning tree by a 1-tree. What is the smallest number of disjoint 1-trees creates a Hamiltonian graph? What is the smallest number of disjoint 1-trees creates a graph containing a shortest Hamiltonian cycle?
Keywords: 1-trees; cycle; Hamitonian path; spanning trees

 Drupal
Drupal CSI of Charles University
CSI of Charles University