 login/create account
login/create account
Hamitonian path
What is the smallest number of disjoint spanning trees made a graph Hamiltonian ★★
Author(s): Goldengorin
We are given a complete simple undirected weighted graph 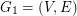 and its first arbitrary shortest spanning tree
and its first arbitrary shortest spanning tree 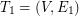 . We define the next graph
. We define the next graph 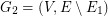 and find on
and find on 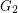 the second arbitrary shortest spanning tree
the second arbitrary shortest spanning tree 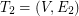 . We continue similarly by finding
. We continue similarly by finding 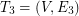 on
on 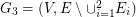 , etc. Let k be the smallest number of disjoint shortest spanning trees as defined above and let
, etc. Let k be the smallest number of disjoint shortest spanning trees as defined above and let 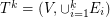 be the graph obtained as union of all
be the graph obtained as union of all  disjoint trees.
disjoint trees.
Question 1. What is the smallest number of disjoint spanning trees creates a graph 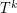 containing a Hamiltonian path.
containing a Hamiltonian path.
Question 2. What is the smallest number of disjoint spanning trees creates a graph 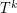 containing a shortest Hamiltonian path?
containing a shortest Hamiltonian path?
Questions 3 and 4. Replace in questions 1 and 2 a shortest spanning tree by a 1-tree. What is the smallest number of disjoint 1-trees creates a Hamiltonian graph? What is the smallest number of disjoint 1-trees creates a graph containing a shortest Hamiltonian cycle?
Keywords: 1-trees; cycle; Hamitonian path; spanning trees

 Drupal
Drupal CSI of Charles University
CSI of Charles University