 login/create account
login/create account
polynomial algorithm
Finding k-edge-outerplanar graph embeddings ★★
Author(s): Bentz
Conjecture It has been shown that a  -outerplanar embedding for which
-outerplanar embedding for which  is minimal can be found in polynomial time. Does a similar result hold for
is minimal can be found in polynomial time. Does a similar result hold for  -edge-outerplanar graphs?
-edge-outerplanar graphs?
 -outerplanar embedding for which
-outerplanar embedding for which  is minimal can be found in polynomial time. Does a similar result hold for
is minimal can be found in polynomial time. Does a similar result hold for  -edge-outerplanar graphs?
-edge-outerplanar graphs? Keywords: planar graph; polynomial algorithm
Approximation ratio for k-outerplanar graphs ★★
Author(s): Bentz
Conjecture Is the approximation ratio for the Maximum Edge Disjoint Paths (MaxEDP) or the Maximum Integer Multiflow problem (MaxIMF) bounded by a constant in  -outerplanar graphs or tree-width graphs?
-outerplanar graphs or tree-width graphs?
 -outerplanar graphs or tree-width graphs?
-outerplanar graphs or tree-width graphs? Keywords: approximation algorithms; planar graph; polynomial algorithm
Approximation Ratio for Maximum Edge Disjoint Paths problem ★★
Author(s): Bentz
Conjecture Can the approximation ratio 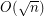 be improved for the Maximum Edge Disjoint Paths problem (MaxEDP) in planar graphs or can an inapproximability result stronger than
be improved for the Maximum Edge Disjoint Paths problem (MaxEDP) in planar graphs or can an inapproximability result stronger than 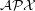 -hardness?
-hardness?
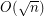 be improved for the Maximum Edge Disjoint Paths problem (MaxEDP) in planar graphs or can an inapproximability result stronger than
be improved for the Maximum Edge Disjoint Paths problem (MaxEDP) in planar graphs or can an inapproximability result stronger than 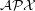 -hardness?
-hardness? Keywords: approximation algorithms; Disjoint paths; planar graph; polynomial algorithm
P vs. NP ★★★★
Problem Is P = NP?
Keywords: Complexity Class; Computational Complexity; Millenium Problems; NP; P; polynomial algorithm
Subset-sums equality (pigeonhole version) ★★★
Author(s):
Problem Let 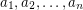 be natural numbers with
be natural numbers with 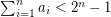 . It follows from the pigeon-hole principle that there exist distinct subsets
. It follows from the pigeon-hole principle that there exist distinct subsets 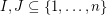 with
with 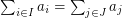 . Is it possible to find such a pair
. Is it possible to find such a pair 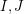 in polynomial time?
in polynomial time?
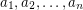 be natural numbers with
be natural numbers with 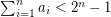 . It follows from the pigeon-hole principle that there exist distinct subsets
. It follows from the pigeon-hole principle that there exist distinct subsets 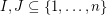 with
with 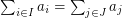 . Is it possible to find such a pair
. Is it possible to find such a pair 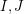 in polynomial time?
in polynomial time? Keywords: polynomial algorithm; search problem
The stubborn list partition problem ★★
Author(s): Cameron; Eschen; Hoang; Sritharan
Problem Does there exist a polynomial time algorithm which takes as input a graph  and for every vertex
and for every vertex 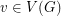 a subset
a subset 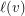 of
of 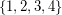 , and decides if there exists a partition of
, and decides if there exists a partition of 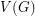 into
into 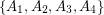 so that
so that 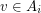 only if
only if 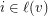 and so that
and so that 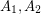 are independent,
are independent, 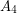 is a clique, and there are no edges between
is a clique, and there are no edges between 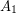 and
and  ?
?
 and for every vertex
and for every vertex 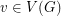 a subset
a subset 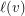 of
of 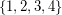 , and decides if there exists a partition of
, and decides if there exists a partition of 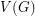 into
into 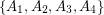 so that
so that 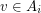 only if
only if 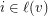 and so that
and so that 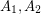 are independent,
are independent, 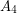 is a clique, and there are no edges between
is a clique, and there are no edges between 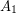 and
and  ?
? Keywords: list partition; polynomial algorithm

 Drupal
Drupal CSI of Charles University
CSI of Charles University